Определение действующего значения переменного напряжения: Действующее значение переменного напряжения

Действующее значение напряжения

В проводниках переменного тока основные электродинамические показатели постоянно изменяются. Вследствие этого возникает вопрос: как можно адекватно оценить напряжение и силу тока в конкретной электроцепи? Так как моментальные и простые усредненные значения недостаточны для полной характеристики электротока, в электродинамике вводят такое понятие, как действующее значение тока.

• Что такое действующее значение напряжения
• Действующее значение тока
• Какие коэффициенты характеризуют переменное напряжение
• Параметры переменного тока
• Формула действующего значение тока

Что такое действующее значение напряжения

Изменение значений переменного тока обычно описывается синусоидальной линией с определенным периодом (Т) и амплитудой напряжения (Um). Кроме напряжения, электрический ток также характеризуется силой (I) и мощностью (P). Для постоянного электротока эти параметры складываются в простую формулу:

P = U × I.

При имеющемся сопротивлении в цепи и с учетом закона Ома (I = U / R) мощность, расходуемую электропотребителем. Можно определить как отношение квадрата напряжения к сопротивлению:

P = U2 / R.

В случае же переменного тока не все так однозначно. С изменением напряжения изменяется и мощность — в каждый момент времени (t) значения отличаются друг от друга. В такой ситуации для оценки электротока удобнее всего использовать его мощностные и тепловые характеристики. Поэтому действующее значение переменного тока приравнивается к работе постоянного тока, производимой за временной промежуток одного периода переменного тока.

При существующей активной нагрузке, независящей от частоты тока и напряжения мгновенная мощность определяется по формуле:

P(t) = U(t) × I(t) = U2 / R

Введя амплитудное значение напряжения, и учитывая период синусоидальной функции, мгновенную мощность можно определить следующим образом:

P(t) = (Um × sin(2π × 1/T))2 / R

Однако этот параметр для переменного тока — не имеет особой важности. Для практических расчетов обычно берут мощность, усредненную за период. Как раз этот показатель указывается на бытовых электроприборах.

Формула усредненной мощности:

Здесь же представлена формула расчета действующего напряжения.

В вышеприведенной формуле интегрирование квадратной величины с последующим извлечением корня дает понять, почему эффективная величина напряжения также носит название «среднеквадратичной». При этом интегральное выражение под корнем является усредненной мощностью, пропорциональной сопротивлению.

Относительно синусоиды напряжение это интегральное выражение упрощается до формулы:

Именно эти цифры показывают вольтметры, настроенные на измерение проводников переменного тока.

Действующее значение тока

Применив метод интегрирования к квадратам амплитудной силы тока и синусу круговой частоты и выведя среднеквадратичные величины, можно получить действующее значение силы тока:

org/ImageObject»>

Сравнивая тепловые эффекты постоянного и переменного электротоков, взятые за одинаковый временной отрезок и при одинаковой активной нагрузке, можно обнаружить, что равенство тепловых характеристик проводников того и другого типа достигается в том случае, если сила линейного тока будет меньше максимальных силовых значений в цепи переменного тока в 1,414 раз.

Какие коэффициенты характеризуют переменное напряжение

Помимо базовых параметров переменного тока, в электротехнике принято производить измерения электросигналов, включая выходные напряжения выпрямителей и импульсы различной формы.

Амплитудное значение напряжения

Под амплитудным или пиковым напряжением подразумевают максимальный показатель U за один период синусоиды:

Um = max(|u(t)|)

Для измерения данного параметра обычно используют вольтметр импульсного типа или осциллограф.

Мгновенное значение тока

Параметр обозначает силу тока или напряжение в конкретный временной момент (u(t), i(t)). В зависимости от динамики электрического сигнала, для определения мгновенных значений могут применяться малоинерционные вольтметры, а также шлейфовые или электронно-лучевые осциллографы.

Среднее значение

Показатель является постоянной составляющей переменного тока. Для напряжения оно рассчитывается по следующей интегральной формуле:

Для синусоидного напряжения с симметричной формой среднее значение равно нулю. Это можно определить с помощью обычного вольтметра. В геометрическом виде это может быть выражено как отношение разности площадей с обеих сторон оси t к периоду. Под названием напряжения смещения величина часто применяется в радиоэлектронике и обозначает напряжение, прилагаемое к электроду для выработки конкретных параметров постоянного электротока.

Среднеквадратичное значение

Среднеквадратичные интегральные величины силы тока и напряжения используются достаточно часто, вследствие их удобства для практического определения электродинамических характеристик в реальных проводниках.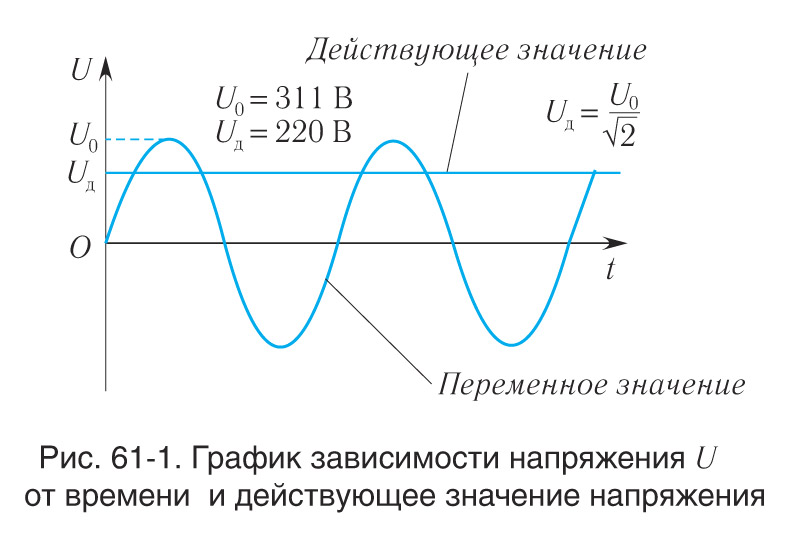 Они основываются на сравнении работы постоянного и переменного тока с активной нагрузкой и определенными величинами U и I.

К примеру, лампочка или обогреватель будут выполнять одинаковую работу по освещению или обогреву как в сети переменного тока со стандартным напряжением 220 В, так и в цепи постоянного тока, если на нее подать такое же напряжение.

Напряжение в электросети обычно выражают в среднеквадратичном исчислении. Большинство приборов, измеряющих силу тока и напряжение, спроектированы под действующие показатели. Отдельные типы амперметров и вольтметров способны показывать верные эффективные значения только для синусоидального тока. В универсальных устройствах, работающих с любыми формами электросигнала, измерение осуществляется с помощью термопреобразователя. При этом фиксируется температура нагревателя, создающего определенное сопротивление.

Кроме того, в измерительных приборах может быть реализован метод возведения в квадрат мгновенного значения, после чего величина усредняется по временному периоду, а затем выводится квадратный корень.

Средневыпрямленное значение

Величина определяется как взятое по модулю среднеарифметическое всех мгновенных значений напряжения. Для одного периода средневыпрямленная величина равна сумме площадей сверху и снизу оси времени. Хотя параметр не находит практического применения, именно он фиксируется по факту большинством измеряющих устройств магнитоэлектрического принципа действия, несмотря на то, что их шкалы имеют градацию для действительных значений. При этом эффективные и средневыпрямленные значения оказываются близки друг к другу только в случае синусоидального напряжения.

Параметры переменного тока

Синусоидальные гармоники являются типичной характеристикой переменного тока. В этом отношении по синусоиде происходит изменение электродвижущей силы и тока при определенной нагруженности цепи. При этом динамика ЭДС может быть описана следующими параметрами:

• Период — время, за которое электродинамические показатели изменяются по полному циклу. Он напрямую связан с частотой вращения роторного механизма генератора электротока.

• Частота — определяется как число периодов за одну единицу времени. Современные стандарты для электросетей предписывают частоту переменного тока в 50 герц. Это означает, что за 1 секунду ток меняет направление 50 раз, а один период длится 20 миллисекунд.

• Амплитуда — максимальная величина гармоники переменного тока. В строгом смысле параметр применим исключительно к синусоидальному изменению. С некоторыми допущениями амплитуда может быть определена и для других форм электросигнала. За один период электродвижущая сила дважды доходит до пиковых значений и обозначается как Em+ и Em- соответственно положению полупериодов.

• Угловая частота — скорость колебательного движения, измеряемая в радианах в секунду. При этом один период синусоиды приравнивается к значению 2π. Общая формула угловой частоты: ω = 2π / Т.

• Фаза колебаний — стадия синусоидальной волны, принимаемая как аргумент функции тока, которая отсчитывается от среднего нулевого значения. Величина фазы колебаний, используемая для определения синуса или косинуса фазового угла, описывается формулой φ = ωt.

Как в случае со среднеквадратичными значениями тока и напряжения, через основные характеристики определяется и среднее значение ЭДС, которое сводится к следующему выражению:

Формула действующего значение тока

Среднеквадратичные показатели переменного тока определяется как отношение амплитудного значения тока к корню из 2.

Схожим образом обозначаются эффективные значения напряжения и ЭДС.

Действительные значения синусоидального тока помогают производить практическую оценку и описание электроцепей. Несмотря на сложность составляющих понятий, эти величины сводятся к простым выражениям. Номинальное напряжение электрических сетей и приборов представляет собой как раз среднеквадратичное значение. Умножив указанный вольтаж на корень из 2, можно узнать амплитудное значение напряжения электроустройств.

Понравилась статья? Расскажите друзьям:

Оцените статью, для нас это очень важно:

Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.

Действующее значение тока. Действующее значение напряжения

Details

08 March 2017

Господа, в прошлой статье мы говорили про мощность и работу переменного тока. Напомню, что тогда мы считали ее через некоторый интеграл, а в самом конце статьи я вскользь сказал, что существуют способы облечения и без того нелегкой жизни и часто можно обойтись вообще без взятия интеграла, если знать про действующее значение тока. Сегодня про него и поговорим!

Господа, вероятно, для вас не станет секретом, что в природе существует большое число видов переменного тока: синусоидальный, прямоугольный, треугольный и так далее. И как их вообще можно сравнивать между собой? По форме? Хмм…Пожалуй, да. Они же визуально различаются, с этим не поспоришь. По частоте? Тоже да, но иногда это вызывает вопросы. Некоторые считают, что само определение частоты применимо исключительно для синусоидального сигнала и его нельзя использовать, например, для последовательности импульсов. Возможно, формально они и правы, но я не разделяю их точку зрения. А еще как еще можно? А, например, по деньгам! Неожиданно? Напрасно. Ток ведь стоит денег. Вернее, стоит денег работа тока. В конце концов ведь те самые киловатт·часы, за которые вы все платите каждый месяц по счетчику не что иное, как работа тока. А поскольку деньги вещь серьезная, то ради такого стоит и термин отдельный ввести. И для сравнения между собой токов различной формы по количеству работы ввели понятие действующего тока.

Итак, действующее (или среднеквадратичное) значение переменного тока – это такая величина некоторого постоянного тока, который за время, равное периоду переменного тока выделит столько же тепла на резисторе, что и наш переменный ток. Звучит очень хитро и, скорее всего, если вы читаете это определение в первый раз, то вряд ли вы его поймете. Это нормально. Когда я его в первый раз услышал в школе, я сам долго доходил, что же это значит. Поэтому сейчас я постараюсь разобрать это определение поподробнее, чтобы вы поняли, что за этой мудреной фразой скрывается быстрее, чем я в свое время.

Итак, у нас есть переменный ток. Допустим, синусоидальный. У него своя амплитуда А_m и период T_период (ну или частота f). На фазу в данном случае пофиг, считаем ее равной нулю. Этот переменный ток течет через некоторый резистор R и на этом резисторе выделяется энергия. За один период T_период нашего синусоидального тока выделится вполне определенное количество джоулей энергии. Это число джоулей мы можем точно посчитать по формулам с интегралом, которые я приводил в прошлый раз. Допустим, мы насчитали, что за один период T_период синусоидального тока выделится Q джоулей тепла. А теперь, внимание, господа, важный момент! Давайте мы заменим переменный ток на постоянный, причем выберем его такой величины (ну то есть столько ампер), чтобы на том же самом резисторе R за то же самое время T_период выделилось ровно такое же количество джоулей Q. Очевидно, мы должны как-то определить величину этого самого постоянного тока, эквивалентного переменному с энергетической точки зрения. И вот когда мы найдем эту величину, то она-то как раз и будет тем самым действующим значением переменного тока. А теперь, господа, вернитесь еще разок к тому мудреному формальному определению, которое я давал вначале. Сейчас оно стало лучше понятно, не так ли?

Итак, суть вопроса, надеюсь, стала понятной, поэтому давайте все сказанное выше переведем на язык математики. Как мы уже писали в прошлой статье, закон изменения мощности переменного тока равен

Количество выделившейся энергии при работе тока за время T_период – соответственно, равно интегралу за время периода T_период:

Господа, теперь нам надо взять этот интеграл. Если по причине нелюбви к математике вам это кажется чем-то слишком мудреным, вы волне можете пропустить выкладки и посмотреть сразу результат. А у меня что-то сегодня настроение вспомнить молодость и аккуратненько разобраться со всеми этими интегральчиками .

Итак, как его нам брать? Ну, величины I_m² и R являются константами и их можно сразу вынести за знак интеграла. А для квадрата синуса нам надо применить формулу понижения степени из курса тригонометрии. Надеюсь, вы ее помните . А если нет, то напомню еще раз:

Погнали считать!

Теперь давайте разобьем интеграл на два интеграла. Можно воспользоваться тем, что интеграл от суммы или разности равен сумме или разности интегралов. В принципе, это очень даже логично, если вспомнить про то, что интеграл – это площадь.

Итак, имеем

Господа, у меня есть для вас просто отличнейшая новость. Второй интеграл равен нулю!

Почему это так? Да просто потому, что интеграл любого синуса/косинуса на величине, кратной его периоду, равен нулю. Полезнейшее свойство, кстати! Рекомендую его запомнить. Геометрически это тоже понятно: первая полуволна синуса идет выше оси абсцисс и интеграл от нее больше нуля, а вторая полуволна идет ниже оси абсцисс, поэтому его величина меньше нуля. А по модулю они равны между собой, поэтому их сложение (собственно, интеграл за весь период) даст в итоге нолик.

Итак, отбрасывая интеграл с косинусом, получаем

Ну и не надо быть большим гуру математики, чтобы сказать, что этот интеграл равен

И, таким образом, получаем ответ

Это мы получили количество джоулей, которое выделится на резисторе R при протекании через него синусоидального тока амплитудой I_m в течении периода T_период. Теперь, чтобы найти чему в данном случае равен действующий ток нам надо исходить из того, что на том же самом резисторе R за то же самое время T_период выделится то же самое количество энергии Q. Поэтому мы можем записать

Если не совсем понятно, откуда здесь взялась левая часть, рекомендую вам повторить статью про закон Джоуля-Ленца. А мы тем временем выразим действующее значение тока I_{действ.} из этого выражения, предварительно сократив все, что можно

Вот такой вот результат, господа. Действующее значение переменного синусоидального тока в корень из двух раз меньше его амплитудного значения. Хорошо запомните этот результат, это важный вывод.

Вообще говоря никто не мешает по аналогии с током ввести действующее значение напряжения. При этом у нас зависимость мощности от времени примет вот такой вид

Именно его мы будем подставлять под интеграл и выполнять все преобразования. Господа, каждый из вас может на досуге при желании это проделать, я же просто приведу конечный результат, поскольку он полностью аналогичен случаю с током. Итак, действующее значение напряжения синусоидального тока равно

Как видим, аналогия полнейшая. Действующее значения напряжения точно также в корень из двух раз меньше амплитуды.

Подобным образом можно рассчитать действующее значение тока и напряжения для сигнала абсолютно любой формы: надо только лишь записать закон изменения мощности для этого сигнала и выполнить пошагово все вышеописанные преобразования.

Все вы, наверняка, слышали, что у нас в розетках напряжение 220 В. А каких вольт? У нас ведь теперь есть два термина – амплитудное и действующее значение. Так вот, оказывается, что 220 В в розетках – это действующее значение! Вольтметры и амперметры, включаемые в цепи переменного тока показывают именно действующие значения. А форму сигнала вообще и его амплитуду в частности можно посмотреть с помощью осциллографа. Ну, мы же уже говорили, что всем интересны деньги, то бишь работа тока, а не какая-то там непонятная амплитуда. Тем не менее давайте-ка все-таки определим, чему равна амплитуда напряжения в наших с вами сетях. Пользуясь только что написанной формулой, можно записать

Отсюда получаем

Вот так вот, господа. В розетках у нас, оказывается, синус с амплитудой аж 311 В, а не 220, как можно было подумать сначала. Что бы убрать все сомнения представлю вам картинку, как выглядит закон изменения напряжения в наших розетках (помним, что частота сети равна 50 Гц или, что тоже самое, период равен 20 мс). Этот закон представлен на рисунке 1.

Рисунок 1 – Закон изменения напряжения в розетках

И специально для вас, господа, я посмотрел напряжение в розетке с помощью осциллографа. Смотрел я его через делитель напряжения 1:5. То есть форма сигнала полностью сохранится, а амплитуда сигнала на экране осциллографа будет в пять раз меньше, чем на самом деле в розетке. Зачем я так сделал? Да просто потому, что из-за большого размаха входного напряжения картинка целиком не влезает на экран осциллографа.

ВНИМАНИЕ! Если у вас нет достаточного опыта работы с высоким напряжением, если вы абсолютно четко не представляете себе как могут течь токи при измерениях в гальванически не отвязанных от сети цепях, настоятельно не рекомендую проводить подобный эксперимент самостоятельно, это опасно! Дело в том, что при подобных измерениях с помощью осциллографа, подключенного к розетке с заземлением есть очень большой шанс что произойдет короткое замыкание через внутренние земли осциллографа и прибор сгорит без возможности восстановления! А если делать эти измерения с помощью осциллографа, подключенного к розетке без заземления, на его корпусе, кабелях и разъемах может присутствовать смертельно опасный потенциал! Это не шутки, господа, если нет понимания, почему это так, лучше этого не делать, тем более, что осциллограммы уже сняты и вы можете их наблюдать на рисунке 2.

Рисунок 2 – Осциллограмма напряжения в розетке (делитель 1:5)

На рисунке 2 мы видим, что амплитуда синуса составляет около 62 вольт, а частота – ровно 50 Гц. Помня, что мы смотрим через делитель напряжения, который делит входное напряжение на 5, мы можем рассчитать реальную величину напряжения в розетке, она равна

Как мы видим, результат измерения очень близок к теоретическому, не смотря на погрешность измерения осциллографа и неидеальность резисторов делителя напряжения. Это свидетельствует о том, что все наши расчеты верны.

На этом на сегодня все, господа. Сегодня мы узнали, что такое действующий ток и действующее напряжение, научились их рассчитывать и проверили результаты расчетов на практике. Спасибо что прочитали это и до новых статей!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Social button for Joomla

Анализ генерации переменного тока: эффективные значения, фазовый угол и частота

Анализ процесса производства электроэнергии переменного тока и переменного тока, который мы используем почти во всех аспектах нашей жизни, необходим для лучшего понимания того, как мощность переменного тока используется в современных технологиях.

Действующие значения

Выходное напряжение генератора переменного тока можно выразить двумя способами. Один из них — графически с использованием синусоиды (рис. 3). Второй способ — алгебраически по уравнению e = E _max sin ωt, которые будут рассмотрены далее в тексте.

Рисунок 3: Синусоида напряжения

Когда напряжение создается генератором переменного тока, результирующий ток изменяется пропорционально напряжению. Когда катушка генератора вращается на 360°, выходное напряжение проходит один полный цикл. За один цикл напряжение увеличивается от нуля до E в одном направлении, уменьшается до нуля, увеличивается до E _max в обратном направлении (отрицательное E _max ), а затем снова уменьшается до нуля. Значение Е _max возникает при 90° и называется пиковым напряжением. Время, за которое генератор совершает один цикл, называется периодом, а количество циклов в секунду называется частотой (измеряется в герцах).

Одним из способов обозначения напряжения или тока переменного тока является пиковое напряжение (E _p ) или пиковый ток (I _p ). Это максимальное напряжение или ток для синусоидальной волны переменного тока.

Другое значение, значение размаха (E _p-p или I _p ), представляет собой величину напряжения или диапазона тока, охватываемого синусоидой. Однако значение, наиболее часто используемое для переменного тока, является эффективным значением. Эффективное значение переменного тока — это количество переменного тока, которое производит такой же эффект нагрева, как и равное количество постоянного тока.

Проще говоря, эффективное значение одного ампера переменного тока будет выделять в проводнике такое же количество тепла в заданное время, как один ампер постоянного тока. Нагревательный эффект данного переменного тока пропорционален квадрату тока. Эффективное значение переменного тока можно рассчитать, возведя в квадрат все амплитуды синусоиды за один период, взяв среднее значение этих значений, а затем извлекая квадратный корень. Эффективное значение, являющееся корнем среднего (среднего) квадрата токов, известно как среднеквадратичное или среднеквадратичное значение. Чтобы понять значение эффективного тока, приложенного к синусоиде, обратитесь к рисунку 4.9.0003

Значения I нанесены на верхнюю кривую, а соответствующие значения I ² нанесены на нижнюю кривую. Кривая I ²  имеет вдвое большую частоту, чем I, и изменяется выше и ниже новой оси. Новая ось представляет собой среднее значение значений I ² , а квадратный корень из этого значения представляет собой среднеквадратичное значение или эффективное значение тока. Среднее значение равно ½ I _max ² . Тогда среднеквадратичное значение равно

. Существует шесть основных уравнений, которые используются для преобразования значения напряжения или тока переменного тока в другое значение, как указано ниже.

• Среднее значение = пиковое значение x 0,637
• Действующее значение (RMS) = пиковое значение x 0,707
• Пиковое значение = среднее значение x 1,57
• Действующее значение (RMS) = среднее значение x 1,11
• Пиковое значение = эффективное значение (RMS) x 1,414
• Среднее значение = эффективное (RMS) x 0,9

Обычно встречающиеся значения тока (I) и напряжения (E) считаются среднеквадратичными значениями; поэтому индекс не используется.

Рисунок 4: Действующее значение тока

Еще одним полезным значением является среднее значение амплитуды в течение положительной половины цикла.

Уравнение ниже представляет собой математическое соотношение между I _av  , I _max и I. 07 av , E _max и E.

E _av = 0,637 E _max   = 0,9 E

Пример 1:

Пиковое значение напряжения в цепи переменного тока составляет 200 В. Каково среднеквадратичное значение напряжения?

E   =  0,707E _макс.

E = 0,707 x 200 = 141,4 В

Чему равно среднее значение силы тока в цепи?

I _av  =  0,637 I _max

I _av  = 0,637 x 10 = 6,37 ампер

Фазовый угол

Фазовый угол — это доля цикла в градусах, прошедшая с момента прохождения напряжением или током заданного значения. Заданное значение обычно равно нулю. Возвращаясь к рисунку 3, примем точку 1 за начальную точку или нулевую фазу. Фаза в точке 2 составляет 30°, в точке 3 — 60°, в точке 4 — 90° и так далее до точки 13, где фаза равна 360° или нулю. Чаще используется термин «разность фаз».

Рис. 5: Соотношение фаз

Разность фаз можно использовать для описания двух различных напряжений с одинаковой частотой, которые проходят через нулевые значения в одном и том же направлении в разное время. На рис. 5 углы по оси обозначают фазы напряжений e ₁ и e ₂ в любой момент времени.

При 120° e ₁ проходит через нулевое значение, которое на 60° опережает e ₂   ( e ₂  равно нулю при 180°). Говорят, что напряжение e ₁ ведет e ₂ на 60 электрических градусов, или можно сказать, что e ₂ отстает от e ₁ на 60 электрических градусов.

Разность фаз также используется для сравнения двух разных токов или тока и напряжения. Если разность фаз между двумя токами, двумя напряжениями или напряжением и током составляет ноль градусов, говорят, что они «синфазны». Если разность фаз отличается от нуля, говорят, что они «не совпадают по фазе».

Расчет напряжения

Приведенное ниже уравнение представляет собой математическое представление напряжения, связанного с любой конкретной ориентацией катушки (индуктора).

e = E _max sinθ

где

e = ЭДС индукции
E _max  = максимальная ЭДС индуцирования θ = угол от точки отсчета (градусы или радианы) Пример 10:993 9000

Что ЭДС индукции в катушке создает максимальную ЭДС 120 В, когда угол от точки отсчета составляет 45 °?

e = E _max sinθ

e = 120 В Sin (45)

e = 84,84 В

Максимальное индуцированное напряжение также можно назвать пиковым напряжением E _p . Если (t) — время, за которое катушка поворачивается на угол (θ), то угловая скорость (ω) катушки равна θ/t и выражается в радианах/сек.

Приведенное ниже уравнение является математическим представлением угловой скорости.

θ = ωt

где

ω = угловая скорость (радиан/сек)
t = время поворота на угол от точки отсчета (сек)
θ = угол от точки отсчета (радианы)

Используя законы подстановки, соотношение между индуцированным напряжением и максимальным индуцированным напряжением , а угловая скорость может быть выражена.

Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между индуцируемым напряжением, максимальным напряжением и угловой скоростью и равно выходной мощности генератора переменного тока.

e = E _max sin(ωt)

где
e = ЭДС индукции (вольт)
E _max = максимальная ЭДС индукции (вольт)
ω = угловая скорость (радиан/с) t 9017 время поворота на угол от точки отсчета (сек)

Расчет тока

Максимальный индуцированный ток рассчитывается аналогичным образом. Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между максимальным индуцированным током и угловой скоростью.

i = I _max sin(ωt)

где

i = индукционный ток (ампер) = время поворота на угол от точки отсчета (сек)

Расчет частоты

Частота переменного напряжения или тока может быть напрямую связана с угловой скоростью вращающейся катушки. Единицы угловой скорости — радианы в секунду, а 2π радиан — это полный оборот.

Радиан — это угол, опирающийся на дугу, равную радиусу окружности. Один радиан равен 57,3 градуса. Один цикл синусоидальной волны генерируется, когда катушка вращается на 2π радиан.

Приведенное ниже уравнение представляет собой математическое соотношение между частотой (f) и угловой скоростью (ω) в цепи переменного тока.

ω = 2πf

где

ω = угловая скорость (радиан/с)
f = частота (Гц)

Найдите: 1. Угловую скорость 2. Угол отсчета в 1 мс 3. ЭДС индукции в этой точке

Решение:

1. ω = 2πf

ω = 2 (3,14) (60 Гц) = 376,8 рад/с 6,8 радиан/сек) ( 0,001 сек)  = 0,3768 радиан

3. e = E _max sinθ

e = (120 В) (sin 0,3768 радиан)
e = (120 В) (0,3679 0,3679)

Будьте первым, кто получит эксклюзивный контент прямо на вашу электронную почту.

Обещаем не спамить. Вы можете отписаться в любое время.

Недействительный адрес электронной почты

Среднее и среднеквадратичное значение переменного тока и напряжения

Среднее и среднеквадратичное значение переменного тока и напряжения: В системе постоянного тока напряжение и ток постоянны, и поэтому нет проблем с указанием их величина. Но в случае системы переменного тока переменное напряжение или ток меняется от момента к моменту, и поэтому возникает проблема, как указать величину переменного напряжения или тока. Переменное напряжение или ток можно выразить через пиковое (максимальное) значение, среднее (среднее) значение или эффективное (среднеквадратичное) значение.

При указании переменного напряжения или тока его пиковое или максимальное значение редко используется, поскольку оно принимает это значение только дважды в каждом цикле. Кроме того, нельзя использовать среднее или среднее значение, поскольку оно настолько же положительно, насколько и отрицательно, поэтому среднее значение равно нулю. Хотя можно было бы использовать среднее значение за полупериод, это было бы не столь логичным выбором, как то, что мы найдем эффективное (виртуальное или среднеквадратичное) значение, которое связано с мощностью, развиваемой в сопротивлении переменным напряжением или током.

Среднее значение переменного тока.

Среднее (или среднее) значение переменного тока равно значению постоянного тока, который переносит по любой цепи такой же заряд, какой переносится этим переменным током в течение заданного времени.

Поскольку в случае симметричного переменного тока (т. е. такого, у которого два полупериода в точности одинаковы, синусоидальные или несинусоидальные) среднее или среднее значение за полный цикл равно нулю, следовательно, для таких переменных величин среднее или среднее значение означает значение определяется путем получения среднего значения мгновенных значений только в течение полупериода или одного чередования. Однако для несимметричного переменного тока, как однополупериодного выпрямленного тока, среднее значение означает значение, определяемое путем взятия среднего значения мгновенных значений по всему циклу.

Среднее значение определяется путем измерения длин ряда равноотстоящих ординат и их среднего значения, т.е. i ₁ , i ₂ , i ₃ ….i _n . и т. д., которые являются средними ординатами.

Среднее значение переменного тока,

С помощью интегрального исчисления среднее (или среднее) значение функции f(t) за определенный интервал времени между t ₁ и t ₂ определяется как

…..(1)

Любая функция, цикл которой непрерывно повторяется, независимо от формы волны, называется периодической функцией , например, синусоидальной функцией, а ее среднее значение определяется выражением

      ……(2)

где T – время период периодической функции.

В случае симметричного переменного тока, синусоидального или несинусоидального, среднее значение определяется путем усреднения только одного полупериода или одного чередования.

т. е. для симметричных сигналов

      ……(3)

Среднеквадратичное значение или эффективное значение переменного тока.

Среднеквадратичное или эффективное значение переменного тока или напряжения определяется постоянным током или напряжением, которые при протекании или приложении к данному сопротивлению в течение заданного времени выделяют такое же количество тепла, как и при протекании переменного тока или напряжения или приложено к одному и тому же сопротивлению в течение того же времени.

Рассмотрим переменный ток формы волны, показанной на рис. 2, протекающий через резистор R Ом. Разделите основание одного чередования на n равных частей и пусть середины ординат равны i ₁ , i ₂ i ₃ …i _n , и т.д. 3 ^рд интервал

Теплота, произведенная в течение n ^-го -го интервала

Суммарная теплота, произведенная за время T

Теперь, если I _eff является эффективным током, то теплота, произведенная этим током в джоулях времени. По определению эти два выражения равны

 

 

Следовательно, действующее или виртуальное значение переменного тока или напряжения равно квадратному корню из среднего значения квадратов последовательных ординат, и поэтому оно известно как среднеквадратичное (rms) значение.

Используя интегральное исчисление, среднеквадратичное (СКЗ) или эффективное значение переменной величины за период времени определяется как

       ……(4)0313

Среднее значение синусоидального тока или напряжения.

Среднее значение синусоиды за полный цикл равно нулю. Следовательно, предполагается среднее значение полупериода. Мгновенное значение синусоидального тока определяется выражением

Рассмотрим первый полупериод, т. е. когда он изменяется от

. Получаем,

 

 

Аналогично, E _av = 0,637 E _макс.

Эффективное (СКЗ) значение синусоидального тока или напряжения

Синусоидальный переменный ток представлен как

 

 

 

 

90902  

3 002 Или,       ….

.(6)

 

Аналогично,

Пример 1. Синусоидальный переменный ток частотой 60 Гц имеет максимальное значение 15 ампер.

1. Запишите уравнение для мгновенного значения,
2. Найдите значение тока после 1/200 секунды,
3. Найдите время, полученное до 10 ампер в первый раз, и
4. 99999999999999999 гг.

Решение:

Максимальное значение тока, I _max = 15А

Частота переменного тока, f = 60 Гц

9 0 Мгновенное значение уравнения синусоидальный переменный ток с θ как ноль, когда время равно нулю, задается как

I = I _max sin 2π f t = 15 sin 2π 60 t

= 15 sin 120 π t Анс.

2     Подставляя секунды в выражение

I = 15 sin 120 π t, получаем значение тока после секунды.

= 15 sin 120 π

= 15 sin 0,6 π

= 150,951[/латекс]

=14,266 A Анс.

3     Пусть мгновенное значение тока в первый раз будет 10 А t секунды после этого момента ток равен нулю и становится положительным

10 = 15 sin 120 π t

Или

= 0,001936 секунд Ans.

4     Среднее значение, Ответ.

Пример 2. Переменный синусоидальный ток имеет среднеквадратичное значение 40 А при частоте 50 Гц. Напишите выражение для мгновенного тока и получите его значение через 0,002 с после прохождения максимального положительного значения.

Решение:

Выражение для мгновенного значения переменного синусоидального тока с нулем, когда время равно нулю, задается как

Ответ.

Когда время измеряется от положительного максимального значения, приведенное выше уравнение изменяется на

Ответ.

 

Пример 3. Переменный ток при пропускании через сопротивление, погруженное в воду на 5 минут, только что поднял температуру воды до точки кипения. При пропускании постоянного тока силой 4 ампера через такое же сопротивление при тех же условиях вода закипала за 8 минут. Найдите действующее значение переменного тока.

Решение:

Пусть действующее значение переменного тока, прошедшего через сопротивление, равно I _{действующее значение} ампер.

Тепло, выделяемое при пропускании переменного тока I _rms ампер через сопротивление R, погруженное в воду на 5 минут

Дж     …..(i)

такое же сопротивление R при погружении в воду на 8 минут

Дж     …..(ii)

Поскольку теплота, выделяемая в обоих случаях, одинакова, приравнивая выражения (i) и (ii), получаем

Или Ans.

Пример 4. Переменное напряжение определяется выражением v 141,4 sin 314 t. Найти

1. Частота
2. Среднеквадратичное значение
4. 9 Среднее значение

   20 3 Мгновенное значение напряжения при t равно 3 мс

5. Время, необходимое для того, чтобы напряжение впервые достигло 100 В после прохождения через нулевое значение.

Решение:

Мгновенное значение переменного напряжения определяется выражением

1     Частота определяется коэффициентом времени, деленным на 2 π, поэтому частота

3,90 с.

Пиковое значение переменного напряжения определяется коэффициентом синуса угла времени, следовательно,

В _max = 141,4 В

2     Среднеквадратичное значение заданного переменного напряжения,

Анс.

3      Среднее значение приведенного переменного напряжения,

Отв.