Найти фазу колебаний в момент времени: Как найти начальную фазу колебаний

Фаза колебаний, теория и онлайн калькуляторы

Фаза колебаний, теория и онлайн калькуляторы

Определение

Повторяющиеся движения или процессы называют колебаниями.

Колебательные движения имеют много общих свойств и описываются одинаковыми законами, имея разную физическую природу. Самой важной характеристикой колебаний является их многократная повторяемость через одинаковые промежутки времени. Колебания встречаются во множестве разных физических явлений.

Любую систему, которая может совершать колебания описывают некоторым физическим параметром, отклонение которого от равновесия зависит от времени по периодическому или близкому к периодическому закону. При рассмотрении механических колебаний, например, рассматривая колебания пружинного маятника, такой переменной величиной является смещение груза от положения равновесия и его скорость.

Собственными колебаниями называют колебания, в которых колебательную систему вывели из состояния равновесия и предоставили самой себе. Колебания в такой системе совершаются без воздействия на систему внешних сил.

Самым простым для описания видом колебаний являются гармонические колебания. Гармоническими колебаниями называют колебания, при которых переменная величина изменяется во времени по закону синуса или косинуса. Разные процессы, повторяющиеся через равные промежутки времени (периодические процессы) можно представить в виде совокупности наложенных гармонических колебаний.

Пусть происходят гармонические колебания некоторого параметра $s$, тогда они описываются уравнением:

\[s=A{\cos ({\omega }_0t+\varphi )\ }\ \left(1\right),\]

где $A=s_{max}$ — амплитуда колебаний; ${\omega }_0$ — циклическая (круговая) частота колебаний. Величина $s$ лежит в пределах $-A\le s\le $+A.

Определение фазы колебаний

Определение

Весь аргумент периодической функции (у нас косинуса:$\ ({\omega }_0t+\varphi )$), которая описывает процесс колебаний,
называют фазой колебаний.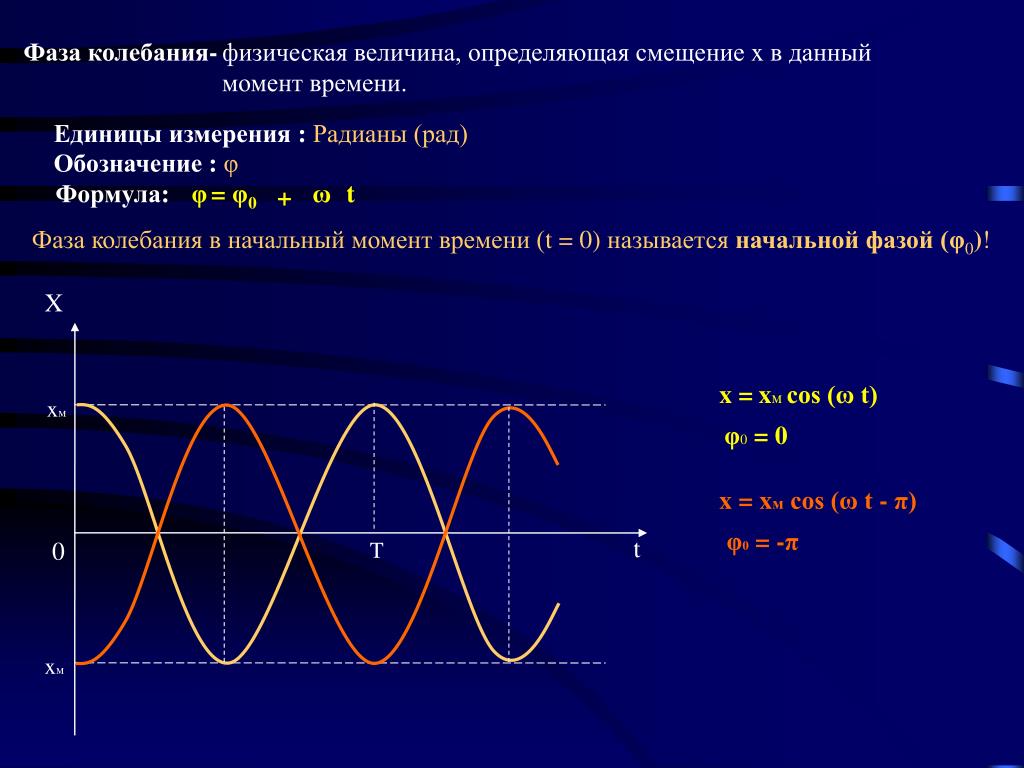 2\left(4\right).\]

Фаза скорости (${\omega }_0t+\varphi +\frac{\pi }{2}$) отличается от фазы ускорения (${\omega }_0t+\varphi +\pi $) на величину равную $\frac{\pi }{2}$. Фаза ускорения отлична от фазы колеблющейся величины на $\pi $. Это значит, что в тот момент времени, когда $s=0$ скорость ее изменения ($\frac{ds}{dt}$) достигает максимального значения. При $s$ равной максимальному отрицательному значению ее ускорение становится наибольшим положительным.

Метод векторных диаграмм

Гармонические колебания можно изображать графически при помощи метода векторных диаграмм (метод вращающейся амплитуды). С этой целью из некоторой точки О на оси X под углом $\varphi $, который равен начальной фазе, откладывают вектор $\overline{A}$. Длина этого вектора равна амплитуде ($A$) колебаний. Если этот вектор приводится во вращение с угловой скоростью ${\omega }_0$, то проекция конца этого вектора перемещается по оси X и принимает значения от $-A$ до $A$, при этом закон колеблющейся величины будет таким, как представляет уравнение (1). Получается, что гармонические колебания можно изобразить при помощи проекции на некоторую ось вектора амплитуды $\overline{A}$, который отложен из произвольной точки этой оси под углом $\varphi $, вращающимся с угловой скоростью ${\omega }_0$ вокруг избранной точки.

Примеры задач на фазу колебаний

Пример 1

Задание. Каким будет отношение кинетической энергии ($E_k$) материальной точки, совершающей колебания вдоль оси X по гармоническому закону, к ее потенциальной энергии ($E_p$), если фаза колебаний равна ${\omega }_0t+\varphi ?$\textit{}

Решение. Уравнение материальной точки, совершающей гармонические колебания, запишем как:

\[x=A{\cos \left({\omega }_0t+\varphi \right)\left(1.1\right).\ }\]

Найдем скорость движения этой точки по оси X:

\[v=\frac{dx}{dt}=-A{\omega }_0{\sin \left({\omega }_0t+\varphi \right)\ }\left(1. 2\left({\omega }_0t+\varphi \right)$

   

Пример 2

Задание. Пружинный маятник (рис.2) совершает колебания, амплитуда которых равна $A$. В момент времени, когда возвращающая сила достигает величины $F$ в первый раз, потенциальная энергия груза на пружине равна $E_p$. Чему равна фаза в этот момент времени. Начальную фазу колебаний принять равной нулю.

Решение. Сила, под воздействием которой пружинный маятник возвращается в положение равновесия — это сила упругости, которая действует на груз со стороны упругой пружины. Считая колебания малыми можно записать закон Гука для возвращающей силы:

\[F=-kx\ \left(2.1\right).\]

где смешение груза из положения равновесия определяете гармоническим законом:

\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\cos ({\omega }_0t)\ }\left(2.2\right),\ }\]

так как по условию $\varphi =0$. 2\left({\omega }_0t\right)}{2kA{cos \left({\omega }_0t\right)\ }}\to \frac{E_p}{F}=-\frac{A}{2}{cos \left({\omega }_0t\right)\to {\omega }_0t\ }=arc{\cos \left(-\frac{2E_p}{FA}\right).\ }\]

Ответ. ${\omega }_0t=arc{\cos \left(-\frac{2E_p}{FA}\right) }$

   

Читать дальше: центр масс.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Фаза колебаний – кратко что это и в чем измеряется, определение, формула, единица измерения в физике

4.6

Средняя оценка: 4.6

Всего получено оценок: 232.

4.6

Средняя оценка: 4.6

Всего получено оценок: 232.

Любой колебательный процесс, который изучается физикой, имеет ряд параметров, одним из которых является фаза. Кратко рассмотрим, что это такое, каков физический смысл фазы, в чем измеряется фаза, приведем формулу фазы колебаний.

Параметры гармонического колебания

Любой колебательный процесс — это изменения некоторого параметра около среднего значения. Колебания бывают периодическими (маятник) и непериодическими (флаг на ветру). Если построить график колебательного процесса, то среднее значение на нём будет представлено горизонтальной прямой, а значение колеблющегося параметра — кривой, постоянно возвращающейся к среднему. При этом для непериодического колебания возвраты будут хаотичными, а для периодического — строго через одинаковый промежуток времени. Этот промежуток называется периодом колебания $T$.

Рис. 1. Периодические и непериодические колебания.

Простейшим периодическим колебанием является колебание, которое совершается по закону круговых функций (синуса или косинуса). Оно называется гармоническим. Поскольку в высшей математике доказывается, что любое колебание (в том числе непериодическое) можно представить в виду бесконечной суммы гармонических колебаний, то в первую очередь изучаются именно они. А по определению любое гармоническое колебание можно представить в виде функции:

$$A=A_0sin \Bigg ( {2\pi\over T} t +\varphi_0 \Bigg ),$$

где:

• $A_0$ — амплитуда колебания, максимальное отклонение мгновенного значения функции от нуля;
• $T$ — период колебаний;
• $t$ — свободная переменная — момент времени, для которого находится мгновенное значение амплитуды;
• $\varphi_0$ — начальная фаза колебаний.

Коэффициент ${2\pi\over T}=\omega$ при свободной переменной $t$ называется угловой частотой. Его физический смысл состоит в том, что это угол, проходимый гармонической функцией за единицу времени. Значение выражения ${2\pi\over T} t +\varphi_0=\varphi$, которое является аргументом функции синуса, называется полной фазой колебания.

Рис. 2. Фаза колебания.

Фаза гармонического колебания

Из формулы гармонического колебания можно понять физический смысл фазы. Поскольку аргументом функции $sin(x)$ является угол поворота единичного вектора на координатной плоскости, выраженный в радианах, и его период равен $2\pi$, то фаза — это часть периода колебания, соответствующая моменту $t$. Она еще выражается в радианах и тоже имеет период $2\pi$.

Из формулы также можно видеть, что если $t=0$, то $\varphi=\varphi_0$ (полная фаза в начальный момент равна начальной фазе).

Разность фаз

Для одного колебательного процесса фаза не играет большой роли. В самом деле, если брать разные моменты времени за начальные, мы можем получать любое значение фазы, колебательный процесс при этом никак не изменится. Однако, когда речь идет о нескольких колебательных процессах, то значение фазы существенно возрастает. Именно фазой определяется разница мгновенных значений двух колебаний.

Рис. 3. Графики колебаний с различными фазами.

Если частоты колебаний неодинаковы, то каждый момент времени фазы будут различны, их разность также будет изменяться. Если же частоты колебаний одинаковы, то несмотря на изменение со временем фазы каждого колебания, разность фаз этих двух колебаний будет постоянной. Это может приводить к интересным ситуациям.

Например, если мы возьмем два колебания с одинаковыми амплитудами и частотами, но у первого начальная фаза будет равна нулю, а у второго — $\pi$, то эти два колебания никогда не будут иметь одинаковых ненулевых значений. Более того, если эти колебания сложить, то их сумма всегда будет равна нулю. Говорят, что такие процессы происходят в противофазе.

Что мы узнали?

Фаза колебания — это часть периода колебания, соответствующая текущему моменту времени. Единица измерения фазы — радиана, она имеет период $2\pi$. Особо важное значение имеет разность фаз двух и более колебаний. Если частота этих колебаний одинакова, то и разность фаз будет всегда постоянной.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 232.

---

А какая ваша оценка?

Гармоническое движение

Гармоническое движение

Говорят, что объект, движущийся вдоль оси X, демонстрирует
простое гармоническое движение , если его положение как функция времени изменяется как

x(t) = x ₀ + A cos(ωt + φ).

Объект колеблется вокруг положения равновесия x ₀ . Если мы
выбираем начало нашей системы координат так, что x ₀ = 0, тогда
смещение x от положения равновесия как функция времени определяется выражением

x(t) = A cos(ωt + φ).

А — амплитуда колебаний,
т. е. максимальное смещение объекта из положения равновесия либо в
положительное или отрицательное направление x. Простое гармоническое движение повторяется.
период
T — время, за которое объект
совершить одно колебание и вернуться в исходное положение.
угловая частота ω определяется как ω = 2π/T.
Угловая частота измеряется в радианах в секунду. Обратная сторона
период частота f = 1/T.
частота f = 1/T = ω/2π движения дает число полных колебаний
в единицу времени. Измеряется в герцах (1 Гц = 1/с).

Скорость объекта как функция времени определяется как

v(t) = -ω A sin(ωt + φ),

а ускорение дается

a(t) = -ω ² A cos(ωt + φ) = -ω ² x.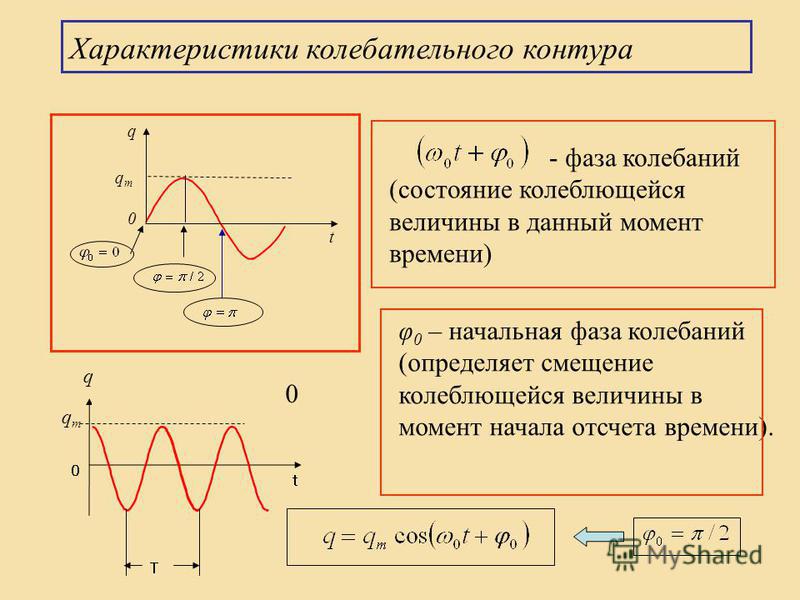

Величина φ называется фазовая постоянная .
Он определяется начальными условиями движения. Если при t = 0
объект имеет максимальное смещение в положительном направлении x, тогда φ = 0, если
он имеет максимальное смещение в отрицательном направлении x, тогда φ = π. Я толстый
t = 0 частица движется через положение равновесия с максимальным
скорость в отрицательном направлении x, тогда φ = π/2. Величина ωt + φ равна
называется фазой .

На рисунке ниже положение и скорость представлены как функция времени.
для колебательного движения с периодом 5 с. Амплитуда и максимальная
скорость имеют условные единицы. Положение и скорость
вне фазы . Скорость равна нулю при максимальном смещении, и
смещение равно нулю на максимальной скорости.

Для простого гармонического движения ускорение a = -ω ² x равно
пропорционально смещению, но в обратном направлении. Простой
гармоническое движение есть ускоренное движение .
Если объект демонстрирует простое гармоническое движение, на него должна действовать сила.
объект. Сила

F = ма = -mω ² х.

Он подчиняется закону Гука , F = -kx, при k = mω ² .

Внешняя ссылка:
Простой
гармоническое движение (Youtube)

---

Сила пружины подчиняется закону Гука. Предположим, что объект
прикреплен к пружине, которая растягивается или сжимается. Тогда пружина давит
сила на объект. Эта сила пропорциональна смещению х тела.
пружинит из положения равновесия и движется в направлении, противоположном
смещение.

Ф = -кх

Предположим, что пружина растянута на расстояние A от положения равновесия, а затем отпущена. Объект
прикрепленный к пружине, ускоряется, возвращаясь к положению равновесия.

a = -(к/м)х

Он набирает скорость по мере продвижения к положению равновесия, потому что его
ускорение направлено в сторону его скорости. Когда он находится в равновесии
положение, ускорение равно нулю, но объект имеет
максимальная скорость. Он выходит за пределы положения равновесия и начинает замедляться.
вниз, потому что ускорение теперь в направлении, противоположном направлению
от его скорости. Пренебрегая трением, он останавливается, когда пружина
сжимается на расстояние А, а затем ускоряется обратно к равновесию
позиция. Он снова промахивается и останавливается в исходном положении, когда
пружина растягивается на расстояние A. Движение повторяется. Объект
колеблется взад и вперед. Он выполняет простое гармоническое движение. Угловой
частота движения

ω = √(к/м),

период

Т = 2π√(м/к),

и частота

f = (1/(2π))√(к/м).

Резюме: Если единственная сила, действующая на тело массой m, является силой закона Гука, F = -kx тогда движение объекта представляет собой простое гармоническое движение. Если x — смещение от равновесия, мы имеем . x(t) = Acos(ωt + φ), v(t) = -ωAsin(ωt + φ), a(t) = -ω 2 Acos(ωt + φ) = -ω 2 x. ω = (к/м) ½ = 2πf = 2π/T. А = амплитуда ω = угловая частота f = частота Т = период φ = фазовая постоянная

Проблема:

Частица совершает простые гармонические колебания, так что ее
перемещение изменяется согласно выражению x = (5 cm)cos(2t + π/6)
где x в сантиметрах, t в секундах. При t = 0 найти
(а) смещение частицы,
(б)
его скорость и
(c) его ускорение.
(г) Найдите период и амплитуду движения.

Решение:

• Рассуждение:
  Анализ простого гармонического движения.
  x(t) = A cos(ωt + φ). A = амплитуда, ω = угловая частота,
  φ = фазовая постоянная.
  v(t) = -ω A sin(ωt + φ), a(t) = -ω ² A cos(ωt + φ) = -ω ² x.
• Детали расчета:
  (a) Смещение как функция времени: x(t) = Acos(ωt +
  ф). Здесь ω = 2/s, φ = π/6, A = 5 см.
  Перемещение при t = 0 равно x(0) = (5 см)cos(π/6) = 4,33 см.
  (b) Скорость при t = 0 равна v(0) = -ω(5 см)sin(π/6) = -5 см/с.
  (c) Ускорение при t = 0 равно a(0) = -ω ² (5
  см)cos(π/6) = -17,3 см/с ² .
  (d) Период движения T =
  2π/ω = π с, а амплитуда равна 5
  см.

Проблема:

Частица массой 20 г движется в простом гармоническом движении с частотой 3
колебаний в секунду и амплитудой 5 см.
(а) Какое общее расстояние проходит частица за один цикл
его движение?
(b)  Какова его максимальная скорость? Где это происходит?
(c) Найдите максимальное ускорение частицы. Где в движении делает
происходит максимальное ускорение?

Решение:

• Рассуждение:
  Проанализируйте простое гармоническое движение, x(t) = A cos(ωt + φ).
• Детали расчета:
  (a) Общее расстояние d, которое проходит частица за один цикл, равно
  от x = -A до x = +A и обратно к x = -A, поэтому d = 4A = 20 см.
  (b) Максимальная скорость частицы
  
  v _макс.
  = ωA = 2πfA = 2π 15 см/с =
  0,94 м/с.
  Частица имеет максимальную скорость при прохождении через
  положение равновесия.
  (c) Максимальное ускорение частицы равно
  до _макс.
  = ω ² А = (2πf) ² А = 17,8 м/с ² .
  
  Частица имеет максимальное ускорение в точках поворота, где
  имеет максимальное водоизмещение.

Предположим, что масса подвешена к вертикальной пружине с жесткостью k. В
равновесия пружина растянута на расстояние x ₀ = мг/к. Если
масса смещается из положения равновесия вниз, а пружина растягивается
дополнительное расстояние x, то полная сила, действующая на массу, равна mg — k(x ₀
+ x) = -kx, направленный в сторону положения равновесия. Если масса
смещен вверх на расстояние x, то полная сила, действующая на массу, равна mg — k(x ₀
— х) = kx, направленный к положению равновесия. Масса будет
выполнять простые гармонические движения. Угловая частота ω = SQRT(k/m) такая же
для массы, колеблющейся на пружине в вертикальном или горизонтальном положении.
Но равновесная длина пружины, вокруг которой она колеблется, различна для
вертикальное положение и горизонтальное положение.

---

Предположим, что объект, прикрепленный к пружине, совершает простое гармоническое движение. Позволять
один конец пружины прикрепите к стене и дайте предмету двигаться горизонтально
на столе без трения.

Какова полная энергия объекта?

Кинетическая энергия объекта

K = ½mv ² = ½mω ² A ² sin ² (ωt
+ ф).

Его потенциальная энергия является упругой потенциальной энергией. Упругий потенциал
энергия, накопленная в пружине, смещенной на расстояние x от положения равновесия
U = ½kx ² . Таким образом, потенциальная энергия объекта равна

.

U = ½kx ² = ½mω ² x ² =
½mω ² A ² cos ² (ωt + φ).

Полная механическая энергия объекта

E = K + U = ½mω ² A ² (sin ² (ωt
+ φ) + cos ² (ωt + φ)) = ½mω ² A ² .

Энергия E в системе пропорциональна квадрат амплитуды .

Е = ½ кА ² .

Это постоянно меняющаяся смесь кинетической и потенциальной энергии.

Для любого объекта, совершающего простое гармоническое движение с угловой частотой ω,
восстанавливающая сила F = -mω ² x подчиняется закону Гука и, следовательно, является
консервативная сила . Мы можем определить потенциальную энергию U = ½mω ² x ² ,
а полная энергия объекта определяется выражением E = ½mω ² А ² . Поскольку v _max = ωA,
мы также можем написать E = ½mv _max ² .

Проблема:

Частица, подвешенная на пружине, совершает колебания с угловой частотой 2
рад/с. Пружина подвешена к потолку кабины лифта и висит
неподвижно (относительно автомобиля) по мере снижения автомобиля с постоянной скоростью 1,5
РС. Затем машина внезапно останавливается. Массой пружины пренебречь.
С какой амплитудой колеблется частица?

Решение:

• Рассуждение:
  При движении в лифте с постоянной скоростью общая сила, действующая на
  масса равна нулю. Сила, действующая на пружину, по величине равна силе
  силы тяжести, действующей на массу, пружина имеет равновесную длину
  вертикальная пружина. Когда лифт внезапно останавливается, конец пружины
  крепятся к потолочным упорам. Однако масса имеет импульс, p = mv,
  и поэтому начинает растягивать пружину. Он движется через
  положение равновесия вертикальной пружины с ее максимальной скоростью v _макс.
  = 1,5 м/с.
  Его скорость как функция времени равна v(t) = -ωAsin(ωt + φ).
• Детали расчета:
  Поскольку v _max = ωA и ω = 2/с, амплитуда амплитуды
  колебания А = 0,75 м.

Проблема:

Система масса-пружина совершает колебания с амплитудой 3,5 см. Если сила
постоянная пружины 250 Н/м и масса 0,5 кг, определить
(а) механическая энергия системы,
(b) максимальная скорость массы и
в) максимальное ускорение.

Решение:

• Рассуждение:
  Механическая энергия системы, совершающей простое гармоническое движение, равна E = ½kA ²
  = ½mω ² А ² .
• Детали расчета:
  (а) Имеем m = 0,5 кг, A = 0,035 м, k = 250 Н/м, ω ²
  = к/м
  = 500/с ² , ω = 22,36/с.
  Механическая энергия системы E = ½kA ²
  = 0,153 Дж.
  (б) Максимальная скорость массы равна v _макс.
  = ωA = 0,78 м/с.
  (c) Максимальное ускорение составляет _макс.
  = ω ² А =
  17,5 м/с ² .

системы координат — Пошаговое руководство по нахождению фазовой постоянной в простом гармоническом движении

По комментариям, в частности:

Конечно! Чтобы уточнить, я изучаю курс под названием «Оптика, волны и современная физика» на втором уровне CEGEP. .. так что, я думаю, это то, что вы будете делать в 12 классе в Штатах? Примером типичной проблемы может быть то, что вам даются некоторые начальные условия (скажем, период и амплитуда осциллятора) и вас просят найти уравнение x(t)=Acos(ωt+φ), используя то, что вы уже знаете. По большей части это нормально, просто используя формулы, но когда дело доходит до решения для φ, я просто не могу этого сделать! Кроме того, мы обычно используем только cos, формулы sin, насколько я знаю, нет.

Я предполагаю, что уровень предшествует университету, и вы не изучали дифференциальные уравнения.

Итак, хотя вы, возможно, и не вывели уравнение математически, вы должны знать, что основное уравнение
$$x=A\cdot \cos(\omega\cdot t + \phi)$$

Итак, вы должны начать писать это уравнение.

После того, как вы его написали, нужно найти значения $A$, $\omega$ и $\phi$. Вероятно, $A$ указан в инструкции. Его также можно найти по графику, если задача дает вам график.

Второе — угловая частота $\omega$. Обычно это находится с помощью периода или «истинной» частоты:

$$ \omega=\frac{2\pi}{T} = 2\pi\nu$$

Опять же, также обычно, что вы должны прочитать период с графика.

---

Теперь, что касается начальной фазы, $\phi$.

В реальной жизни этот параметр иногда не имеет значения. Это потому, что частота достаточно высока, а система колеблется так быстро, что вам все равно, где именно она началась. В конце концов, вы просто наблюдаете за колебаниями, и вам нужно снова решить, где проводить измерения.

Тем не менее, в задачах нужно найти $\phi$. Если в инструкциях запрашивается $\phi$, вы также должны указать его.

А как ты это делаешь? Ну, как я уже сказал, вам нужны дополнительные данные. Вы не можете знать $\phi$ с помощью $A$ и $T$. Вам нужно так называемое граничное условие . То есть положение на данный момент времени. Например:

 при t=2с, x=1м
 

Затем вы возвращаетесь к уравнению и заменяете:

$$x=A\cdot \cos(\omega\cdot t + \phi)\quad \Rightarrow \quad 1m=A\cdot \cos(\omega \cdot 2s + \phi)$$

Убедитесь, что $A$ и $\omega$ уже известны. Вот почему я начал с них. Вы должны сначала вычислить $A$ и $\omega$. Тогда вы можете сделать эту замену.

Граничное условие особенно просто, если оно дает момент $t=0$. Это называется начальным состоянием .

 При t=0, x=0.
 

Затем вы должны подставить и найти $\phi$:

$$0=A\cdot \cos(\omega\cdot 0 + \phi)\quad \Rightarrow \quad \phi=acos(0)=\pi /2$$

Вот как это работает.

---

Но подождите, вы можете сказать: есть и другие решения. И ты прав. Это также может быть $acos(0)=3\pi/2$. Как вы можете сказать?

Ну, по этим данным ничего не скажешь. Вам нужен еще один факт. Дополнительный факт обычно связан со скоростью. Они могут сказать

 При t=0, x=0 и частица увеличивает свое положение.
 

Увеличить позицию — это то же самое, что сказать «положительная скорость». Так что вам также нужно работать с формулой скорости, которая является производной по времени от положения:

$$v=\frac{d}{dt}x=A\cdot\omega\cdot\sin(\omega\cdot t+\phi)$$

Таким образом, вам придется проверить оба решения: $\ пи/2$ и $3\пи/2$.