Содержание
В схеме, изображенной на рисунке, R1=5 Ом, R2=6 Ом, R3=3 Ом, сопротивлением амперметра
Условие задачи:
В схеме, изображенной на рисунке, \(R_1=5\) Ом, \(R_2=6\) Ом, \(R_3=3\) Ом, сопротивлением амперметра и подводящих проводов можно пренебречь. Вольтметр показывает 2,1 В. Каково показание амперметра?
Задача №7.5.48 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_1=5\) Ом, \(R_2=6\) Ом, \(R_3=3\) Ом, \(U=2,1\) В, \(I_1-?\)
Решение задачи:
Если посмотреть на схему, то видно, что ток \(I\) разделяется в узле B на два тока \(I_1\) и \(I_2\):
\[I = {I_1} + {I_2}\;\;\;\;(1)\]
Также на схеме видно, что сопротивление \(R_2\) соединено параллельно с амперметром и сопротивлением \(R_3\), то есть они находятся под одинаковым напряжением. Так как в условии сказано, что сопротивлением амперметра можно пренебречь, то имеем право записать следующее:
\[{I_1}{R_3} = {I_2}{R_2}\]
Выразим отсюда силу тока \(I_2\):
\[{I_2} = {I_1}\frac{{{R_3}}}{{{R_2}}}\;\;\;\;(2)\]
Подставим выражение (2) в формулу (1):
\[I = {I_1} + {I_1}\frac{{{R_3}}}{{{R_2}}}\]
\[I = \frac{{{I_1}\left( {{R_2} + {R_3}} \right)}}{{{R_2}}}\]
Откуда искомая сила тока на амперметре \(I_1\) равна:
\[{I_1} = \frac{{I{R_2}}}{{{R_2} + {R_3}}}\;\;\;\;(3)\]
Отлично, значит теперь нужно найти общую силу тока \(I\), сделать это можно элементарно по закону Ома для участка цепи:
\[I = \frac{U}{R}\;\;\;\;(4)\]
Здесь \(R\) – общее сопротивление цепи, отстоящей от ветви с вольтметром справа. Эта цепь состоит из двух параллельно соединенных сопротивлений \(R_2\) и \(R_3\), которые в свою очередь соединены последовательно с сопротивлением \(R_1\). Поэтому нетрудно понять, что сопротивление \(R\) получится определить по формуле:
\[R = {R_1} + \frac{{{R_2}{R_3}}}{{{R_2} + {R_3}}}\]
Если привести под общий знаменатель, получим:
\[R = \frac{{{R_1}{R_2} + {R_1}{R_3} + {R_2}{R_3}}}{{{R_2} + {R_3}}}\]
Полученное выражение подставим в формулу (4):
\[I = \frac{{U\left( {{R_2} + {R_3}} \right)}}{{{R_1}{R_2} + {R_1}{R_3} + {R_2}{R_3}}}\]
А это выражение подставим в формулу (3):
\[{I_1} = \frac{{U\left( {{R_2} + {R_3}} \right)}}{{{R_1}{R_2} + {R_1}{R_3} + {R_2}{R_3}}} \cdot \frac{{{R_2}}}{{{R_2} + {R_3}}}\]
\[{I_1} = \frac{{U{R_2}}}{{{R_1}{R_2} + {R_1}{R_3} + {R_2}{R_3}}}\]
Отлично, задача решена в общем виде. Подставим численные данные в формулу и посчитаем численный ответ:
\[{I_1} = \frac{{2,1 \cdot 6}}{{5 \cdot 6 + 5 \cdot 3 + 6 \cdot 3}} = 0,2\;А\]
Ответ: 0,2 А.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.5.47 По проводнику сопротивлением 4 Ом в течение 2 минут прошло 500 Кл электричества
7.5.49 Вольтметр, внутреннее сопротивление которого равно 50 кОм, подключенный к источнику
7.5.50 Определите показание амперметра в электрической цепи, изображенной на рисунке
ГДЗ по физике за 9-11 классы к сборнику задач по физике для 9-11 классов составитель Г.Н.Степанова39. Закон Ома для участка цепи. Сопротивление.
Решебники и ГДЗ
Начните вводить часть условия (например, могут ли, чему равен или найти):
- №955. Определите общее сопротивление цепи, изображенной на рисунках 137, 138, 139.
-
№956. Определите сопротивление однородного проволочного каркаса в форме правильного шестиугольника с двумя диагоналями, соединенными в центре (рис. 140).
Сопротивление каждой стороны шестиугольника принять равным R.
- №957. Провода соединены по схеме, изображенной на рисунке 141. Сопротивление каждого из проводов равно 1 Ом. Чему равно сопротивление Raв между точками а и в?
- №958. Определите сопротивление цепи, изображенной на рисунке 142.
- №959. На рисунке 143 показаны два разных способа включения в цепь реостата. Перечислите особенности работы реостата в каждом случае. Каково максимальное сопротивление каждого участка цепи, если сопротивление каждого резистора равно R?
- №960. На рисунке 144 показан способ включения реостата в цепь, как потенциометра. С какой целью прибегают к такому включению?
- №961. На рисунке 145 изображены схемы устройств, называемых ламповыми реостатами. Объясните принцип действия этих реостатов. Есть ли преимущества у какого-либо из приведенных реостатов перед другим? Какие?
- №962. Удлинитель длиной 30 м сделан из медного провода диаметром 1,3 мм. Каково сопротивление удлинителя? Каково падение напряжения на нем, если по нему течет ток 10 А?
-
№963.
Определите сопротивление нити лампы (рис. 146). если вольтметр показывает 50 В, амперметр показывает 0,5 А и внутреннее сопротивление вольтметра равно 40 кОм.
- №964. Две дуговые лампы и добавочный резистор соединены последовательно и включены в сеть напряжением 110 В. Найдите сопротивление добавочного резистора, если падение напряжения на каждой лампочке 40 В, а сила тока в цепи 12 А.
- №965. К источнику тока напряжением 12 В присоединена линия, питающая две лампы. Схема включения ламп показана на рисунке 147. Сопротивление участков линии R1 = = R2 = R3 = R4 = R = 1,5 Ом. Сопротивление каждой лампы 36 Ом. Определите падение напряжения на
- №966. Сопротивление одного из двух последовательно включенных проводников в п раз больше сопротивления другого. Во сколько раз изменится сила тока на участке (напряжение постоянно), если эти проводники включить параллельно?
-
№967. Три одинаковые лампочки соединены по схеме, приведенной на рисунке 148. Как будет изменяться накал каждой из ламп, если эти лампы по одной поочередно выключать? закорачивать? При возможности проверьте ответ на опыте.
- №968. В цепь, состоящую из трех ламп, соединенных по схеме, приведенной на рисунке 148, подано напряжение 90 В. Сила тока, потребляемая от источника, равна 0,5 А. Сопротивление одной из ламп разветвленного участка равно сопротивлению лампы, включенной в н
- №969. В цепи, схема которой изображена на рисунке 149, все сопротивления одинаковы и равны 2 Ом. Найдите распределение токов и напряжений.
- №970. Имеются источник тока напряжением 6 В, реостат сопротивлением 30 Ом и две лампочки, на которых написано: 3,5 В, 0,35 А и 2,5 В, 0,5 А. Как собрать цепь, чтобы лампочки работали в нормальном режиме?
- №971. Найдите распределения сил токов и напряжений в цепи, схема которой изображена на рисунке 150.
- №972. В электрических приборах часто используют мостовые схемы Они работают по принципу компенсации и позволяют сравнить неизвестные величины с известными (стандартными). Одна из таких схем — мостик Уитстона — показана на рисунке 151. Условие компенсации
-
№973.
Определите неизвестное сопротивление в уравновешенной (ток через гальванометр отсутствует) мостовой схеме, изображенной на рисунке 152. Найдите потенциалы точек А и В.
- №974. Определите силу тока в цепи с мостом Уитстона, изображенной на рисунке 153, если R1=2 Ом, R2 — 1 Ом, R3 = 2 Ом, R4=1 Ом, R5=1 Ом, ε = 1 В.
Учебник по физике: комбинированные цепи
Ранее в уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь. Они могут быть соединены посредством последовательных соединений или посредством параллельных соединений. Когда все устройства в цепи соединены последовательным соединением, тогда цепь называется последовательной цепью. Когда все устройства в цепи соединены параллельными соединениями, тогда цепь называется параллельной цепью. Третий тип схемы предполагает двойное использование последовательных и параллельных соединений в цепи; такие схемы называются составными схемами или комбинированными схемами.
При анализе комбинированных цепей крайне важно хорошо понимать концепции, относящиеся как к последовательным, так и к параллельным цепям. Поскольку в комбинированных схемах используются оба типа соединений, понятия, связанные с обоими типами цепей, применимы к соответствующим частям схемы. Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.
 .. .. |
|
Каждое из приведенных выше понятий имеет математическое выражение. Сочетание математических выражений вышеприведенных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной цепи.
Анализ комбинированных цепей
Основная стратегия анализа комбинированных цепей включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной цепи в последовательную. После преобразования в последовательную цепь анализ можно проводить обычным образом.
Этот метод согласуется с формулой
где R 1 , R 2 и R 3 — значения сопротивления отдельных резисторов, соединенных параллельно. Если два или более резистора, находящиеся в параллельных ветвях, не имеют одинакового сопротивления, то необходимо использовать приведенную выше формулу. Пример этого метода был представлен в предыдущем разделе урока 4.
Применяя понимание эквивалентного сопротивления параллельных ветвей к комбинированной цепи, комбинированную цепь можно преобразовать в последовательную цепь. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения полного сопротивления цепи.
Итак, на диаграмме B полное сопротивление цепи равно 10 Ом.
После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже двумя примерами.
Пример 1:
Первый пример — самый простой случай — параллельно расположенные резисторы имеют одинаковое сопротивление. Целью анализа является определение тока на входе и падения напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательных резистора на 8 Ом эквивалентны одному резистору на 4 Ом. Таким образом, два ответвленных резистора (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор на 4 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление равно
Ом.0012 R to = R 1 + 4 Ом + R 4 = 5 Ом + 4 Ом + 6 Ом
R to = 15 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.
я до = 4 ампера
Расчет тока 4 А представляет собой ток в месте расположения батареи. Но резисторы R 1 и R 4 включены последовательно и ток в последовательно соединенных резисторах везде одинаков. Таким образом,
Для параллельных ветвей сумма токов в каждой отдельной ветви равна току вне ветвей. Таким образом, я 2 + I 3 должен равняться 4 Ампер. Существует бесконечное число возможных значений I 2 и I 3 , которые удовлетворяют этому уравнению. Поскольку значения сопротивлений равны, значения тока в этих двух резисторах также равны. Следовательно, ток в резисторах 2 и 3 равен 2 Ампер.
Теперь, когда ток в каждом отдельном резисторе известен, уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждый резистор. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (4 А) • (5 Ом)
ΔV 1 = 20 В
ΔV 2 = I 2 • R 2 = (2 А) • (8 Ом)
ΔV 2 = 16 В
ΔV 3 = I 3 • R 3 = (2 А) • (8 Ом)
ΔV 3 = 16 В
ΔV 4 = I 4 • R 4 = (4 А) • (6 Ом)
ΔV 4 = 24 В
Анализ завершен, и его результаты представлены на диаграмме ниже.
Пример 2:
Второй пример представляет собой более сложный случай — параллельно расположенные резисторы имеют разное значение сопротивления. Цель анализа та же — определить ток на входе и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить по обычной формуле для эквивалентного сопротивления параллельных ветвей: 2 + 1 / R 3 …
1 / R eq = 1 / (4 Ом) + 1 / (12 Ом)
1 / R экв. = 0,333 Ом -1
R экв. = 1 / (0,333 Ом -1 )
R экв. = 3,00 Ом
На основании этого расчета можно сказать, что два ответвленных резистора (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 3 Ом.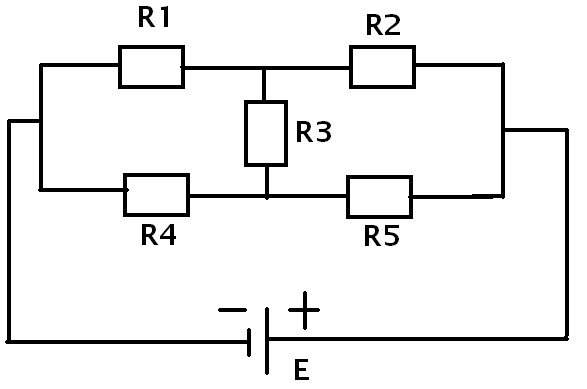
R до = 16 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи. При этом необходимо будет использовать общее сопротивление и общее напряжение (или напряжение батареи).
I to = 1,5 А
Расчет тока 1,5 А представляет собой ток в месте расположения батареи. Но резисторы R 1 и R 4 включены последовательно и ток в последовательно соединенных резисторах везде одинаков. Таким образом,
Для параллельных ветвей сумма токов в каждой отдельной ветви равна току вне ветвей.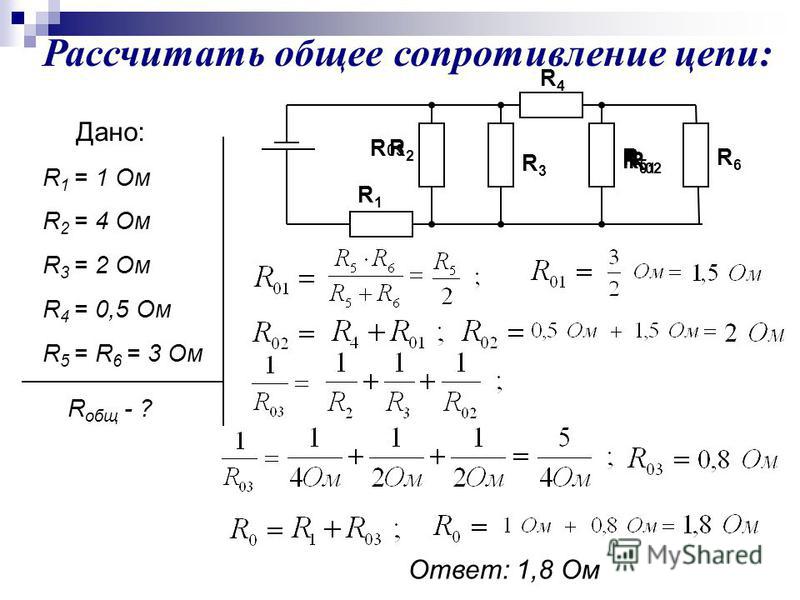
Для определения падения напряжения на параллельных ветвях сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R 1 и R 4 ). Уравнение закона Ома (ΔV = I • R) можно использовать для определения падения напряжения на каждом резисторе.
ΔV 1 = I 1 • R 1 = (1,5 А) • (5 Ом)
ΔV 1 = 7,5 В
ΔВ 4 = I 4 • R 4 = (1,5 А) • (8 Ом)
ΔV 4 = 12 В
Эта схема питается от источника 24 В. Таким образом, кумулятивное падение напряжения заряда, пересекающего петлю цепи, составляет 24 вольта. Будет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R 1 и R 4 ). Падение напряжения на ветвях должно составлять 4,5 вольта, чтобы компенсировать разницу между 24 вольтами и 19 вольтами.Падение 0,5 В на R 1 и R 4 . Таким образом,
Зная падение напряжения на параллельно включенных резисторах (R 1 и R 4 9002 6 ) позволяет использовать уравнение закона Ома ( ΔV = I • R) для определения тока в двух ветвях.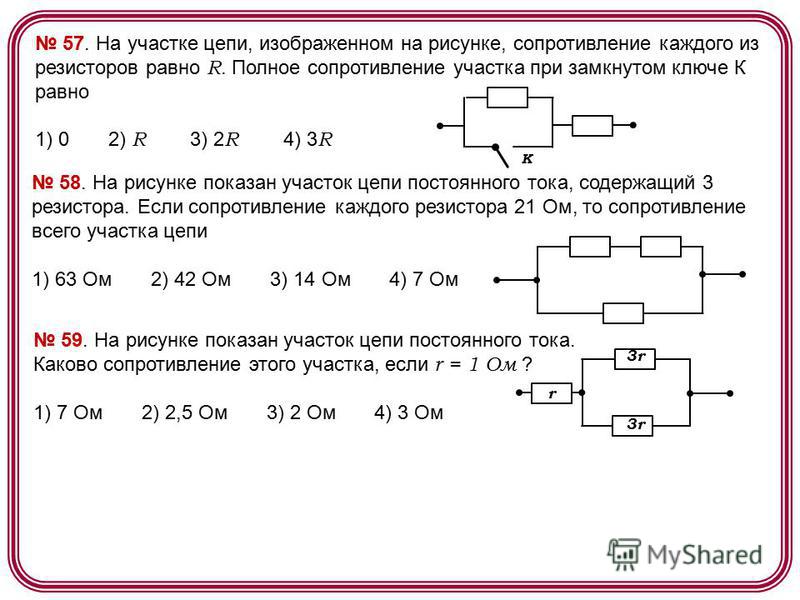
I 2 = ΔV 2 / R 2 = (4,5 В) / (4 Ом)
I 2 = 1,125 А
I 3 = ΔV 3 / R 3 = (4,5 В) / (12 Ом)
I 3 = 0,375 А
Анализ завершен, и его результаты представлены на диаграмме ниже.
Разработка стратегии
Два приведенных выше примера иллюстрируют эффективную концептуальную стратегию анализа комбинационных цепей. Подход требовал твердого понимания последовательностей и параллельных концепций, обсуждавшихся ранее. Такие анализы часто проводятся для решения физической задачи для заданного неизвестного. В таких ситуациях неизвестность обычно варьируется от проблемы к проблеме. В одной задаче номиналы резисторов могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче можно указать ток в батарее и несколько номиналов резисторов, а неизвестная величина станет сопротивлением одного из резисторов.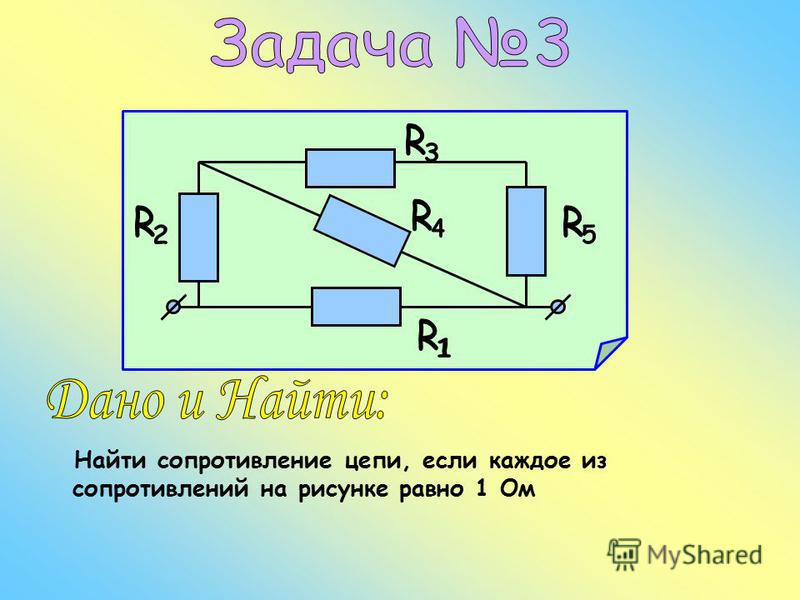
Начинающему ученику предлагаются следующие рекомендации по решению задач комбинированной схемы:
- Если схематическая диаграмма не предоставлена, найдите время, чтобы построить ее. Используйте схематические символы, подобные показанным в примере выше.
- Приступая к проблеме, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записывая известные значения и приравнивая их к символу, такому как I tot , I 1 , R 3 , ΔV 2 и т. д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.
- Знать и использовать соответствующие формулы эквивалентного сопротивления последовательно и параллельно соединенных резисторов.
Использование неправильных формул гарантирует неудачу.
- Превратите комбинированную цепь в строго последовательную, заменив (мысленно) параллельную часть одним резистором, сопротивление которого равно эквивалентному сопротивлению параллельной части.
- Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будут определены с помощью этого уравнения. При его использовании важно подставлять в уравнение соответствующие значения. Например, при расчете I 2 важно подставить в уравнение значения ΔV 2 и R 2 .
Для дальнейшей практики анализа комбинированных цепей рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.
Мы хотели бы предложить …
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom.
Посетите: DC Circuit Builder
Проверьте свое понимание
1. Комбинированная схема показана на схеме справа. Используя схему, ответьте на следующие вопросы.
а. Ток в точке А равен _____ (больше, равно, меньше) току в точке В.
b. Ток в точке B равен _____ (больше, равно, меньше) току в точке E.
в. Ток в точке G равен _____ (больше, равно, меньше) току в точке F.
d. Ток в точке E равен _____ (больше, равно, меньше) току в точке G.
e. Ток в точке B равен _____ (больше, равно, меньше) току в точке F.
f. Ток в точке А равен _____ (больше, равно, меньше) тока в точке L.
g. Ток в точке H равен _____ (больше, равно, меньше) тока в точке I.
2. Рассмотрим комбинированную цепь на схеме справа. Используя схему, ответьте на следующие вопросы. (Считать, что падение напряжения в самих проводах пренебрежимо мало.)
а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.
b. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
в. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.
d. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
ф. Разность электрических потенциалов между точками L и A равна _____ (больше, равно, меньше) разности электрических потенциалов (падению напряжения) между точками B и K.
3. Используйте понятие эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.
4. Проанализируйте следующую цепь и определите значения полного сопротивления, полного тока, а также падения тока и напряжения на каждом отдельном резисторе.
5. По схеме вопроса №4 определите …
а. … номинальная мощность резистора 4.
б. … скорость, с которой энергия потребляется резистором 3.
Series and Parallel — AP Physics 1
Все ресурсы AP Physics 1
7 Диагностические тесты
170 практических тестов
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 Следующая →
AP Физика 1 Справка »
Электричество и волны »
Электричество »
Схемы »
Последовательная и параллельная
Цепь имеет резистор с сопротивлением , за которым следуют три параллельных ответвления, каждое из которых содержит резистор с сопротивлением .
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, нам нужно рассчитать эквивалентное сопротивление трех параллельно соединенных резисторов. Для этого воспользуемся следующим уравнением:
Теперь, чтобы получить полное эквивалентное сопротивление, мы можем просто сложить два оставшихся значения, так как они идут последовательно:
Сообщить об ошибке 5
А напряжение прикладывается к точкам A и B, так что ток течет от A к R2, а затем к B. Какова величина этого напряжения, если ток через R2 равен 4 А?
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, нам нужно рассчитать ток, протекающий через R2 без приложенного дополнительного напряжения.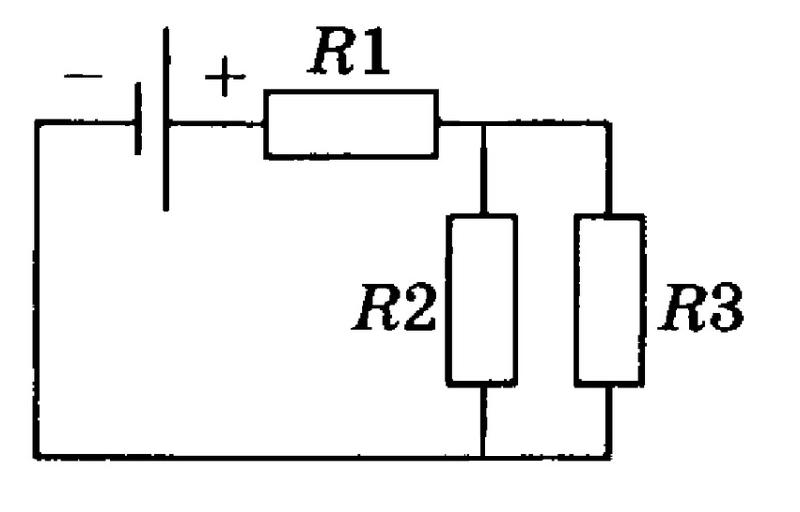
Затем мы можем использовать закон Ома для расчета тока в цепи:
Теперь, когда у нас есть ток, мы можем рассчитать дополнительный ток, который вносит новое напряжение:
На пути нового напряжения есть только один резистор (R2), поэтому мы можем рассчитать, каким должно быть это напряжение для подачи нового тока:
Сообщить об ошибке
9 0005
Каково эффективное сопротивление этой цепи постоянного тока?
Возможные ответы:
Ни один из других ответов
Правильный ответ:
Объяснение:
Во-первых, давайте напомним себе, что эффективное сопротивление последовательно соединенных резисторов равно и эффективное сопротивление параллельно подключенных резисторов равно .
Начните эту задачу с определения эффективного сопротивления резисторов 2, 3 и 4:
(Это потому, что эти три резистора включены последовательно.)
Теперь схему можно упростить до следующего:
Далее нам нужно будет определить эффективное сопротивление резисторов 6 и 9.0005
Опять же, схему можно упростить:
Отсюда можно определить эффективное сопротивление цепи постоянного тока, вычислив эффективное сопротивление резисторов , 1 и 5:
Сообщить об ошибке
Две лампочки, одна из которых имеет класс , а другая – , последовательно подключены к батарее. Какой из них будет ярче? А если их подключить параллельно?
Возможные ответы:
Серия:
Параллельный:
Недостаточно информации для решения этой задачи
Параллельный:
Серийный:
Параллельный:
Правильно ответ:
ряд:
параллельный:
Объяснение:
Первый шаг к решению этой проблемы — выяснить, как сопротивление лампочки соотносится с номинальной мощностью.
Таким образом, существует обратная зависимость между сопротивлением лампочки и номинальной мощностью.
Второй шаг — рассмотреть элементы схемы, соединенные последовательно и параллельно. Последовательно они имеют один и тот же ток; параллельно они делят одно и то же напряжение. Таким образом, для двух последовательно соединенных лампочек ярче будет та, у которой больше сопротивление (меньшая мощность), а для параллельной конфигурации ярче будет лампочка с меньшим сопротивлением (больше мощность).
Сообщить об ошибке
Если у нас есть 3 последовательно соединенных резистора, причем резистор 1 имеет сопротивление , резистор 2 имеет сопротивление , а резистор 3 имеет сопротивление , каково эквивалентное сопротивление серии?
Возможные ответы:
Правильный ответ:
Пояснение:
Общее сопротивление последовательно соединенных резисторов равно сумме их индивидуальных сопротивлений.
Сообщить об ошибке
Вам представлены три резистора, каждый размер . В чем разница между общим сопротивлением резисторов, соединенных последовательно, и полным сопротивлением резисторов, соединенных параллельно?
Возможные ответы:
Правильный ответ:
Объяснение:
Резисторы последовательно:
Параллельные резисторы:
Сообщить об ошибке
Каково общее сопротивление трех резисторов, , , и , включенных параллельно?
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение эквивалентного сопротивления для нескольких резисторов, включенных параллельно:
Подставьте известные значения и решите.
Обратите внимание, что для параллельных резисторов общее сопротивление никогда не превышает сопротивления наименьшего элемента.
Сообщить об ошибке
Цепь создается с использованием батареи и 3-х одинаковых резисторов, как показано на рисунке. Каждый из резисторов имеет сопротивление . Если резистор удалить из цепи, как это повлияет на ток через резистор?
Возможные ответы:
Проходной ток увеличится в два раза
Проходной ток уменьшится
Невозможно определить, не зная удельного сопротивления провода
Проходной ток останется прежним
Проходной ток увеличится на множитель четыре
Правильный ответ:
Ток через уменьшится
Объяснение:
Поскольку резисторы и образуют параллельную сеть, удаление из цепи увеличивает сопротивление этой части цепи.
Сообщить об ошибке
Определите общий заряд, хранящийся в цепи с двумя одинаковыми плоскопараллельными конденсаторами, соединенными параллельно, с площадью и расстоянием между параллельными пластинами. Предположим, что пространство между параллельными пластинами представляет собой вакуум. Схема показывает разницу напряжений 10 В.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы определить общий накопленный заряд, нам нужно сложить емкость каждого конденсатора (поскольку они соединены параллельно) и умножить на разницу напряжений. Напомним, что для конденсаторов
Для конденсаторов с параллельными пластинами:
Здесь, , которая представляет собой диэлектрическую проницаемость пустого пространства, является диэлектрической проницаемостью, которая из-за присутствия только вакуума, , которая представляет собой площадь параллельных пластин, и , что является расстоянием между пластинами.
Подставьте известные значения для определения емкости.
Каждый из двух конденсаторов имеет емкость
Поскольку конденсаторы подключены параллельно, общая емкость представляет собой сумму емкостей каждого из них. Общая емкость в цепи определяется как:
Подставьте это значение в наше первое уравнение и найдите общий накопленный заряд.
, где — общий заряд, хранящийся в конденсаторе. Начиная с
Сообщить об ошибке
Каков общий ток, протекающий через систему с 2 параллельными резисторами с сопротивлением и и аккумулятором с разностью напряжений 10 В?
Возможные ответы:
Правильный ответ:
Объяснение:
Сначала нам нужно определить общее сопротивление цепи, прежде чем мы узнаем, какой ток протекает через нее. Поскольку резисторы подключены параллельно, их сопротивления складываются обратно:
, где — общее сопротивление цепи.
 Сопротивление каждой стороны шестиугольника принять равным R.
Сопротивление каждой стороны шестиугольника принять равным R. Определите сопротивление нити лампы (рис. 146). если вольтметр показывает 50 В, амперметр показывает 0,5 А и внутреннее сопротивление вольтметра равно 40 кОм.
Определите сопротивление нити лампы (рис. 146). если вольтметр показывает 50 В, амперметр показывает 0,5 А и внутреннее сопротивление вольтметра равно 40 кОм.
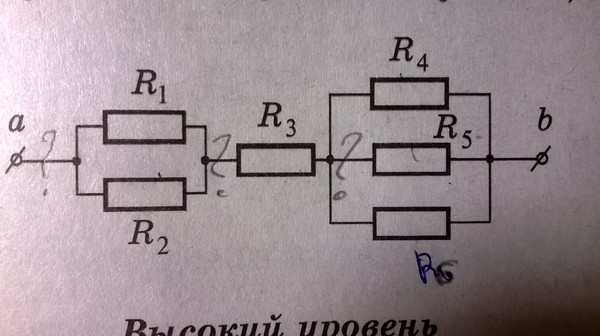 Определите неизвестное сопротивление в уравновешенной (ток через гальванометр отсутствует) мостовой схеме, изображенной на рисунке 152. Найдите потенциалы точек А и В.
Определите неизвестное сопротивление в уравновешенной (ток через гальванометр отсутствует) мостовой схеме, изображенной на рисунке 152. Найдите потенциалы точек А и В. Использование неправильных формул гарантирует неудачу.
Использование неправильных формул гарантирует неудачу. 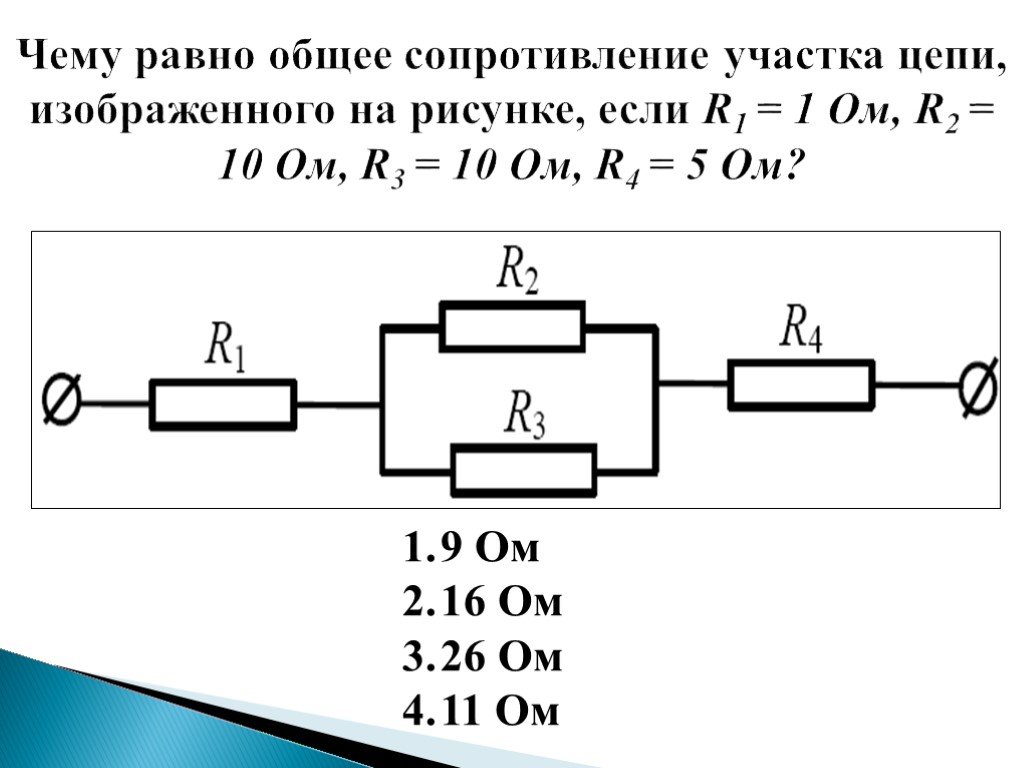
Добавить комментарий