График зависимости силы упругости от деформации: На рисунке представлен график зависимости силы упругости пружины от величины её деформации. Определите жёсткость этой пружины.

Закон Гука, сила упругости — определение, формулы

Покажем, как применять знание физики в жизни

Начать учиться

205.6K

Если вы возьмете резиновый шарик и шар из камня и начнете кидать в стену (скучный день выдался, мало ли) — заметите, что они отталкиваются совершенно по-разному. Про силу упругости, которая объясняет этот процесс — в этой статье.

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.

Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Деформация

Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил

Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.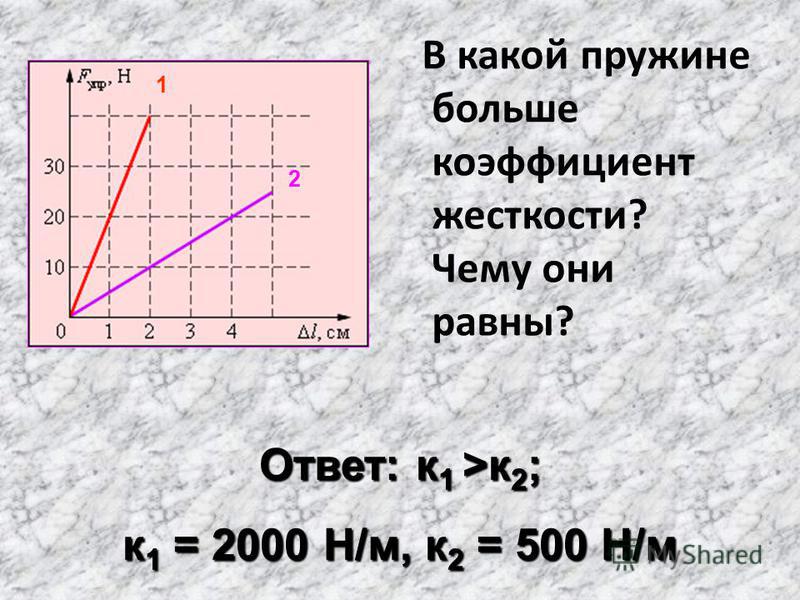

На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу сил. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.

По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:

• Деформация растяжения

• Деформация сжатия

• Деформация сдвига

• Деформация при кручении

• Деформация при изгибе

Сила упругости: Закон Гука

Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать.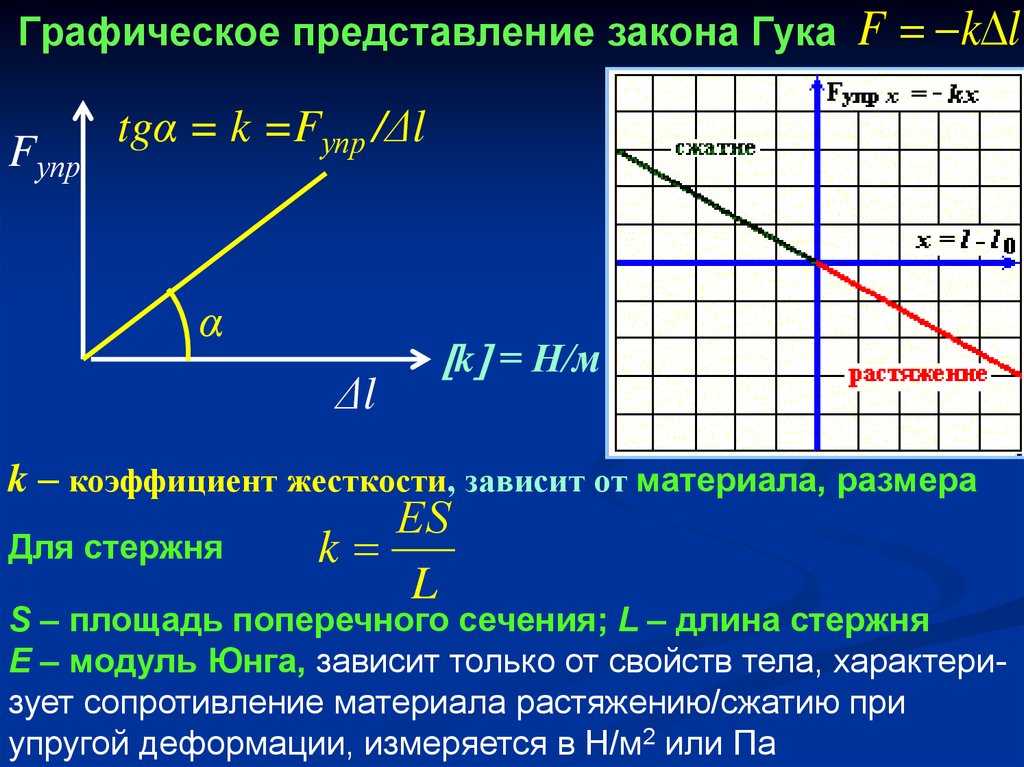 Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.

Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не может вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Какой буквой обозначается сила упругости?

Закон Гука —сила упругости [Н] k — коэффициент жесткости [Н/м] х — изменение длины (деформация) [м]

Важно раз

Изменение длины может обозначаться по-разному в различных источниках.

Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Важно два

Поскольку сила упругости всегда направлена против деформации (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при равномерном (без ускорения) поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу тяжести. Не забываем массу представить в единицах СИ – килограммах.

СИ — международная система единиц.

«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

m = 300 г = 0,3 кг

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

F = mg = 0,3*10 = 3 Н.

Вспомним закон Гука:

И выразим из него модуль удлинения лески:

Так как одна сила уравновешивает другую, мы можем их приравнять:

Подставим числа, жесткость лески при этом выражаем в ньютонах:

= 0,01 м = 1 см

Ответ: удлинение лески равно 1 см.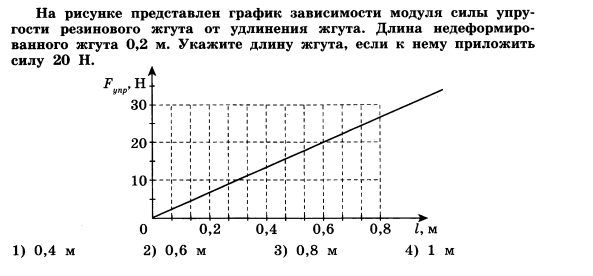

Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Коэффициент жесткости при последовательном соединении пружин k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

В случае когда пружины соединены параллельно величина общего коэффициента жесткости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Коэффициент жесткости при параллельном соединении пружин k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

Задачка

Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.

При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

При последовательном соединении общая жесткость двух пружин

66,7 Н/м

Очень-очень важно!

Не забудь при расчете жесткости при последовательном соединении в конце перевернуть дробь.

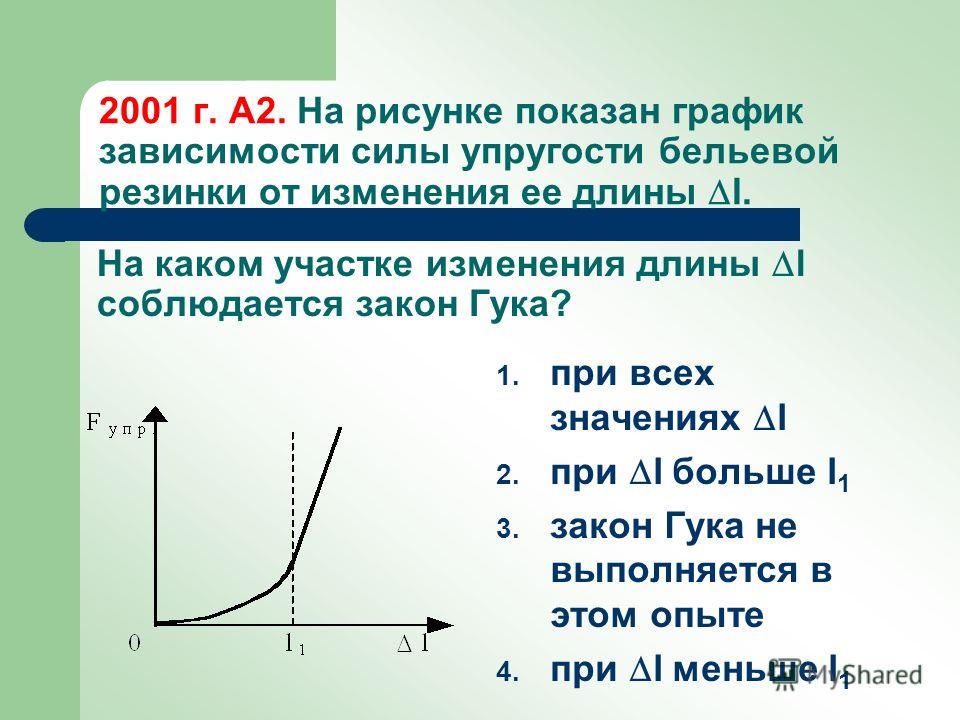
График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

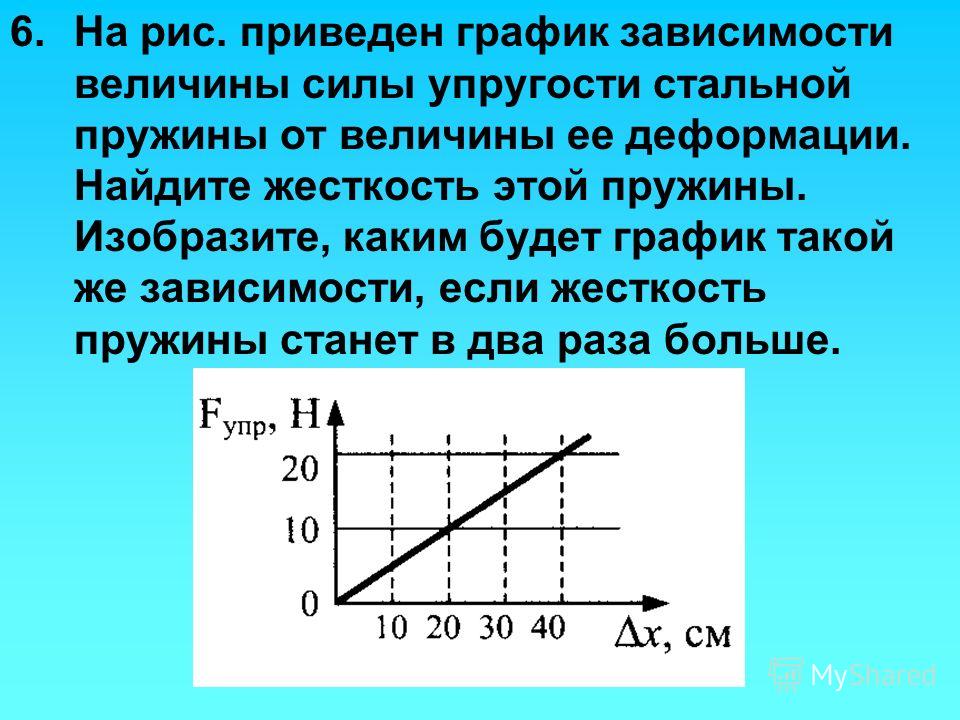
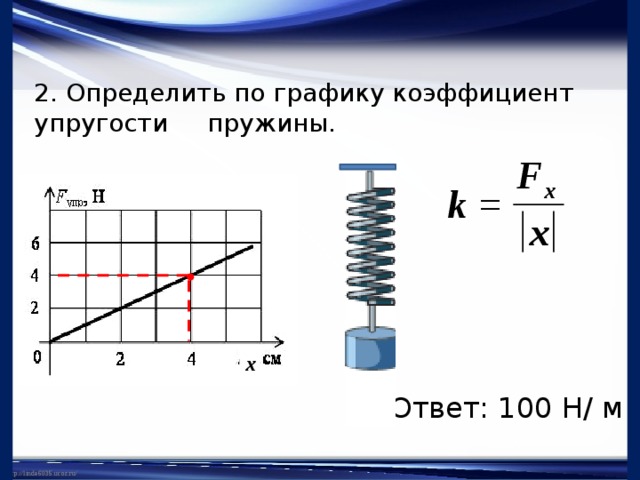
Задачка 1

Определите по графику коэффициент жесткости тела.

Решение:

Из Закона Гука выразим коэффициент жесткости тела:

F = kx

Снимем значения с графика.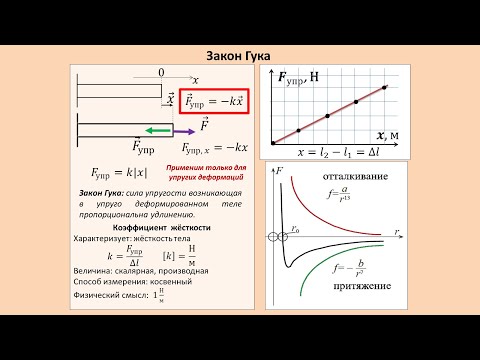 Важно выбрать одну точку на графике и записать для нее значения обеих величин.

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры:

2 см = 0,02 м

И подставим в формулу:

=100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!

Задачка 2

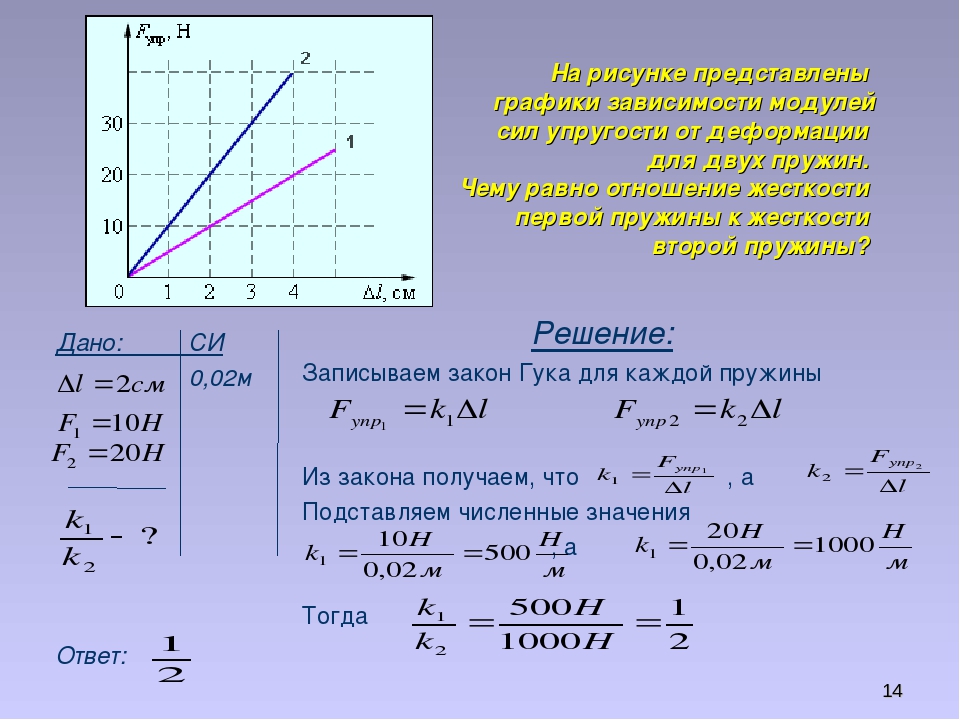
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.

Решение:

Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.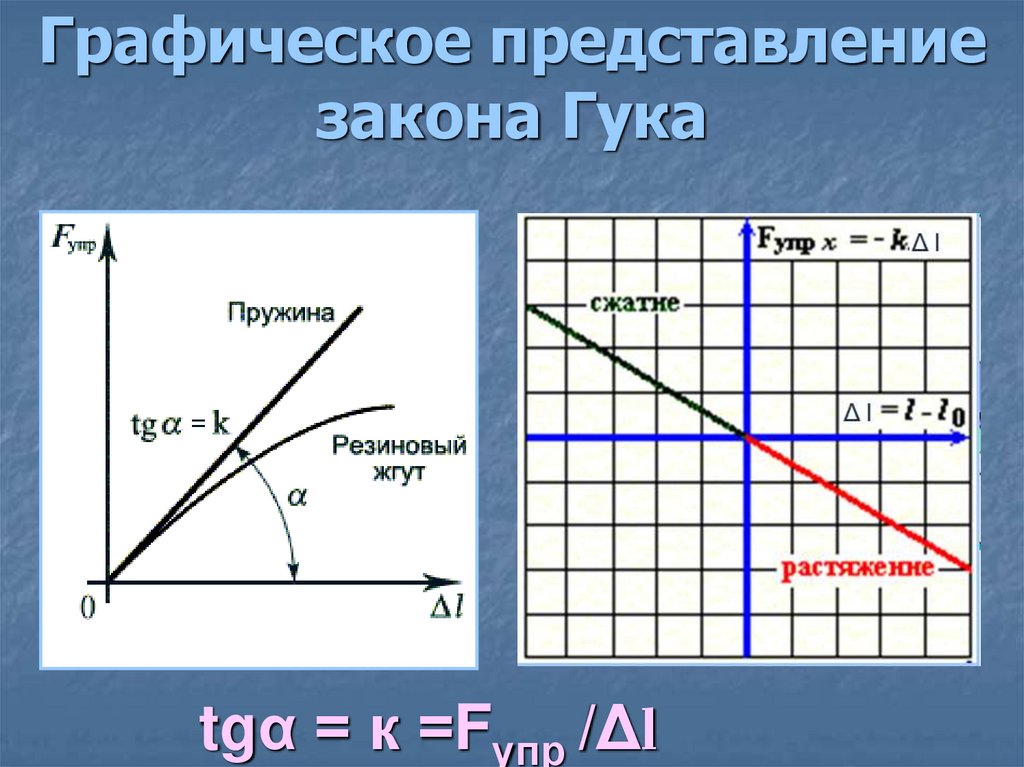

Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.

---

---

Карина Хачатурян

К предыдущей статье

187.3K

Закон электромагнитной индукции

К следующей статье

Момент силы

Получите индивидуальный план обучения физике на бесплатном вводном уроке

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Сила упругости.

Деформация: ее величина и типы. Закон Гука

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.

Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.

 

Деформация.

 

Силы упругости возникают при деформациях тел. Деформация — это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб.
Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.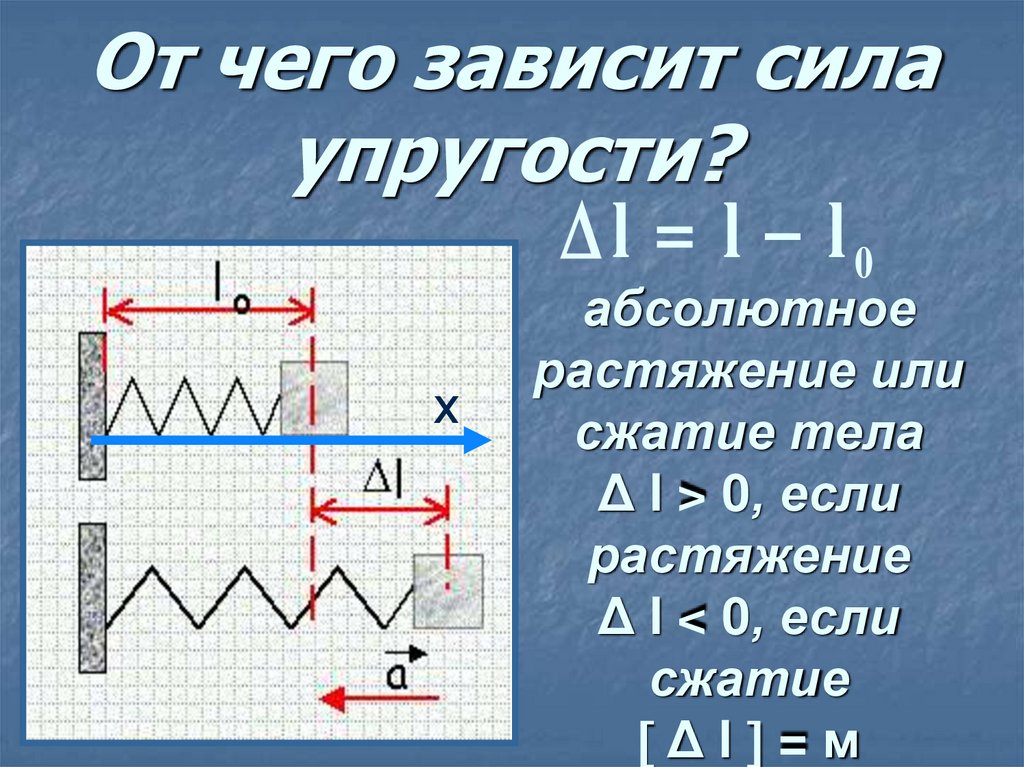

Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.

Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.

Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации.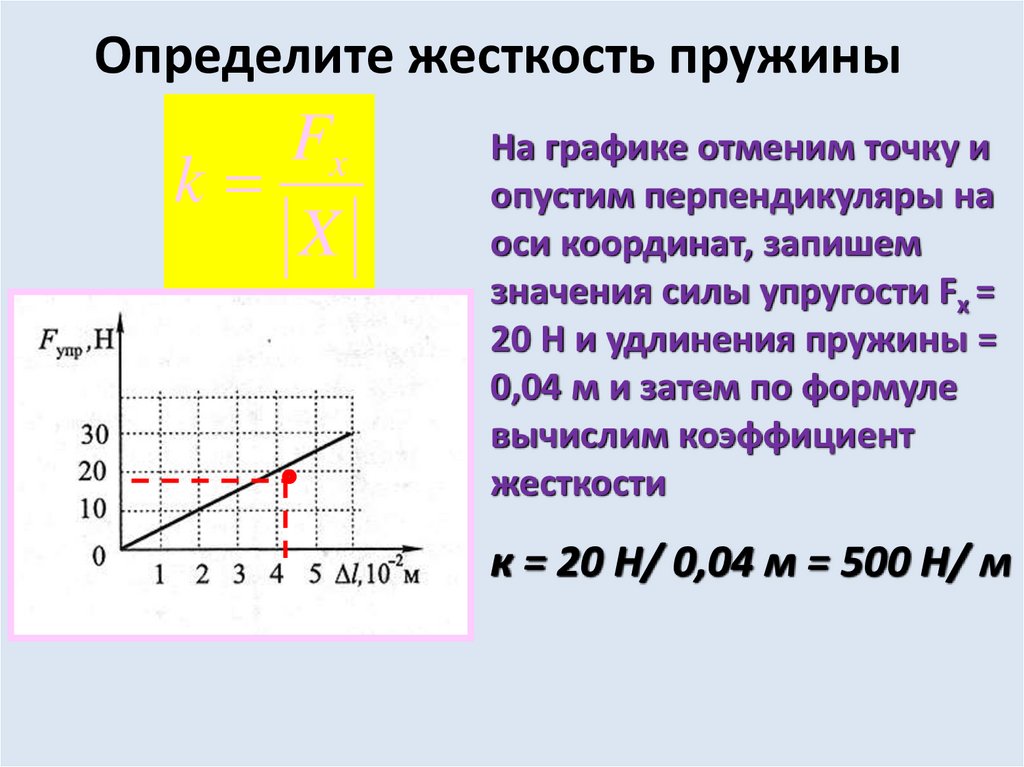 Сила упругости:

1. действует между соседними слоями деформированного тела и приложена к каждому слою;
2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример — сила реакции опоры).

Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил
выходит далеко за рамки школьной программы.

В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.

 

Закон Гука.

 

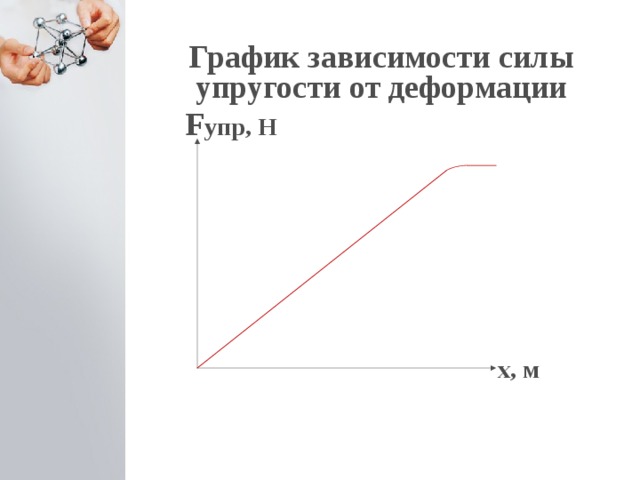
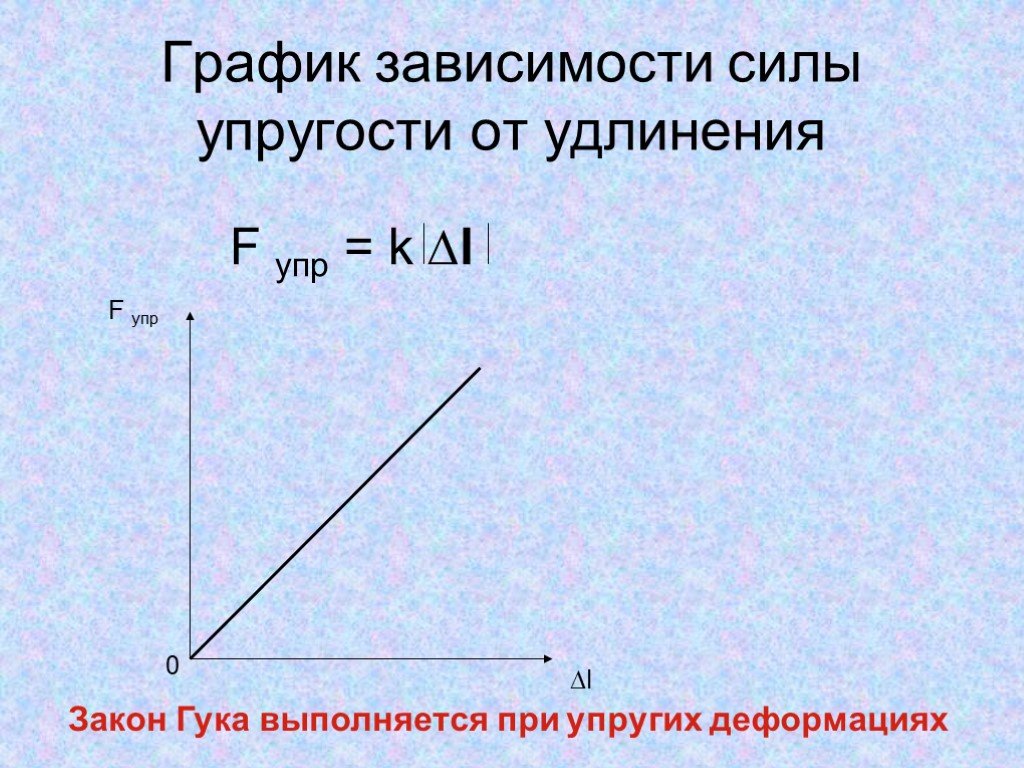
Деформация называется малой, если изменение размеров тела много меньше его первоначальных размеров. При малых деформациях зависимость силы упругости от величины деформации оказывается линейной.

Закон Гука.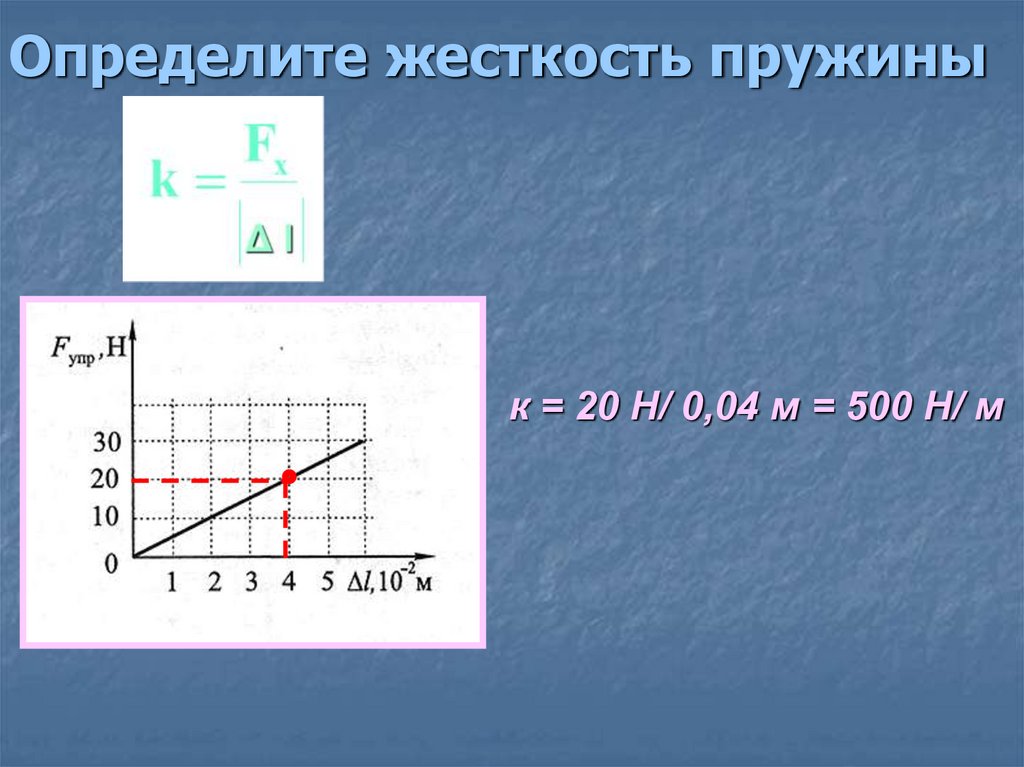 Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину , сила упругости даётся формулой:

(1)

где — коэффициент жёсткости пружины.

Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров.

Из формулы (1) следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):

Рис. 1. Закон Гука

 

Коэффициент жёсткости — о угловой коэффициент в уравнении прямой . Поэтому справедливо равенство:

,

где — угол наклона данной прямой к оси абсцисс. Это равенство удобно использовать при экспериментальном нахождении величины .

Подчеркнём ещё раз, что закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела. Когда деформации перестают быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид. Соответственно, прямая линия на рис. 1 — это лишь небольшой начальный участок криволинейного графика, описывающего зависимость от при всех значениях деформации .

 

Модуль Юнга.

 

В частном случае малых деформаций стержней имеется более детальная формула, уточняющая общий вид ( 1 ) закона Гука.

Именно, если стержень длиной и площадью поперечного сечения растянуть или сжать
на величину , то для силы упругости справедлива формула:

.

Здесь — модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометрических размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.

 

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Сила упругости.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.04.2023

Механика материалов: деформация » Механика гибких конструкций

---

исследования

человек

курсы

блог

---

Штамм

До сих пор мы сосредоточились на напряжении в элементах конструкции. Когда вы прикладываете нагрузку к объекту, он деформируется . Подумайте о резиновой ленте: вы тянете за нее, и она становится длиннее — она растягивается . Деформация — это мера того, насколько объект растянут, и деформация  является отношением между деформацией и исходной длиной.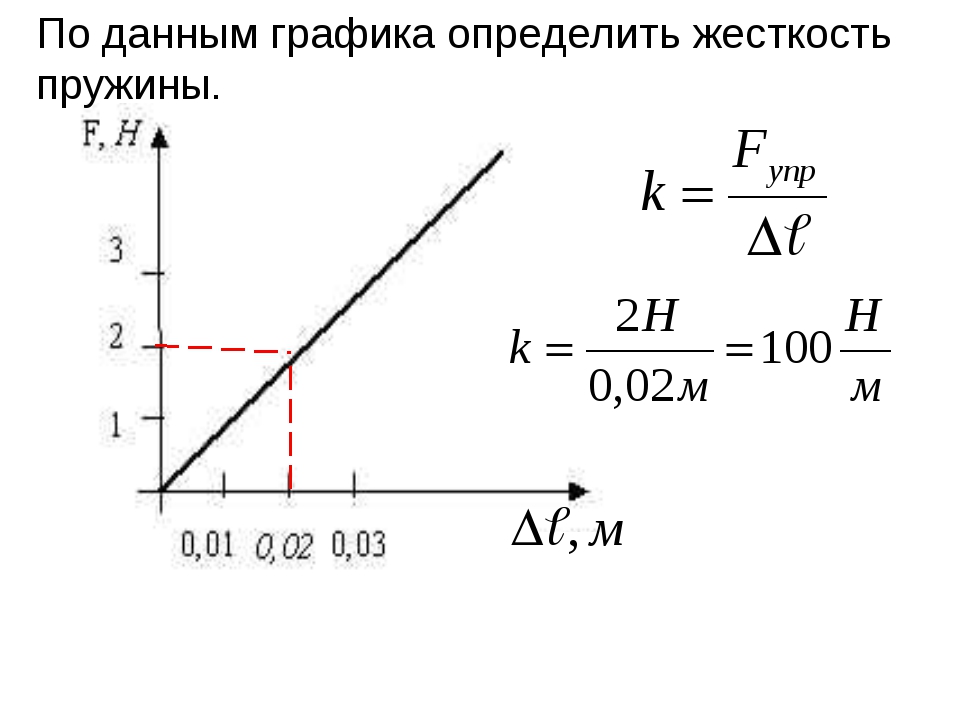 Думайте о деформации как о -процентном удлинении — насколько больше (или меньше) становится объект после его загрузки.

Как и при напряжении, существует два типа деформации, которым может подвергаться конструкция: 1. Нормальная деформация и 2. Деформация сдвига . Когда сила действует перпендикулярно (или «нормально») к поверхности объекта, она создает нормальное напряжение. Когда сила действует параллельно поверхности объекта, возникает напряжение сдвига.

Рассмотрим стержень, находящийся под одноосным растяжением. Стержень удлиняется под действием этого напряжения до новой длины, и нормальная деформация представляет собой отношение этой небольшой деформации к первоначальной длине стержня.

Деформация — это безразмерная мера того, насколько объект становится больше или меньше от приложенной нагрузки. Нормальная деформация  происходит, когда удлинение объекта происходит в ответ на нормальное напряжение (т.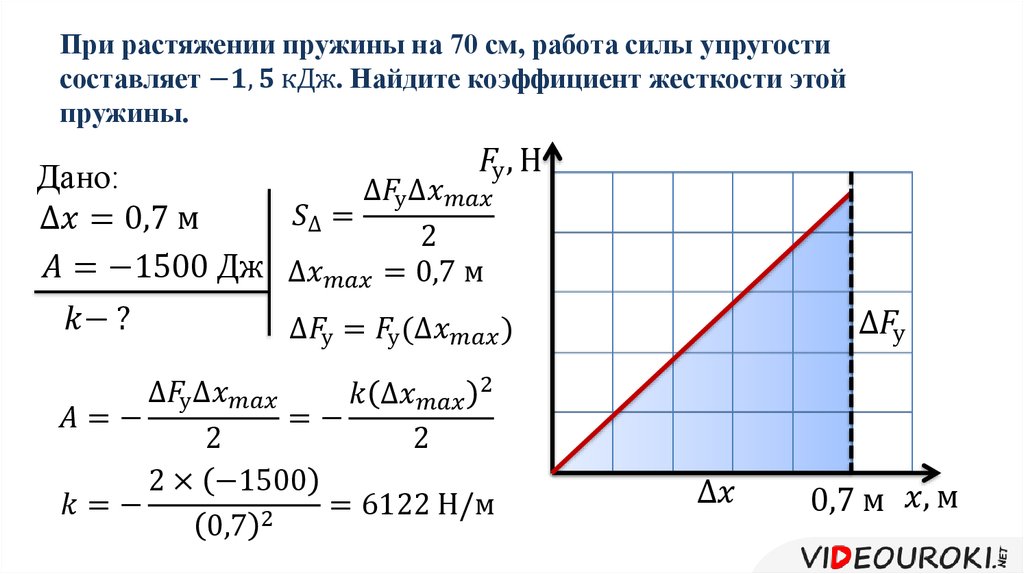 е. перпендикулярно поверхности), и обозначается греческой буквой эпсилон. Положительное значение соответствует растяжению деформации, а отрицательное сжатию . Деформация сдвига возникает, когда деформация объекта является реакцией на напряжение сдвига (т. Е. Параллельно поверхности), и обозначается греческой буквой гамма .

 

Механическое поведение материалов

Очевидно, что стресс и напряжение связаны. Напряжение и деформация связаны конститутивным законом , и мы можем определить их взаимосвязь экспериментально, измерив, какое усилие требуется для растяжения материала. Это измерение может быть выполнено с помощью 9Испытание на растяжение 0015.   В простейшем случае, чем больше вы тянете за объект, тем больше он деформируется, и при малых значениях деформации эта зависимость является линейной. Эта линейная упругая зависимость между напряжением и деформацией известна как закон Гука .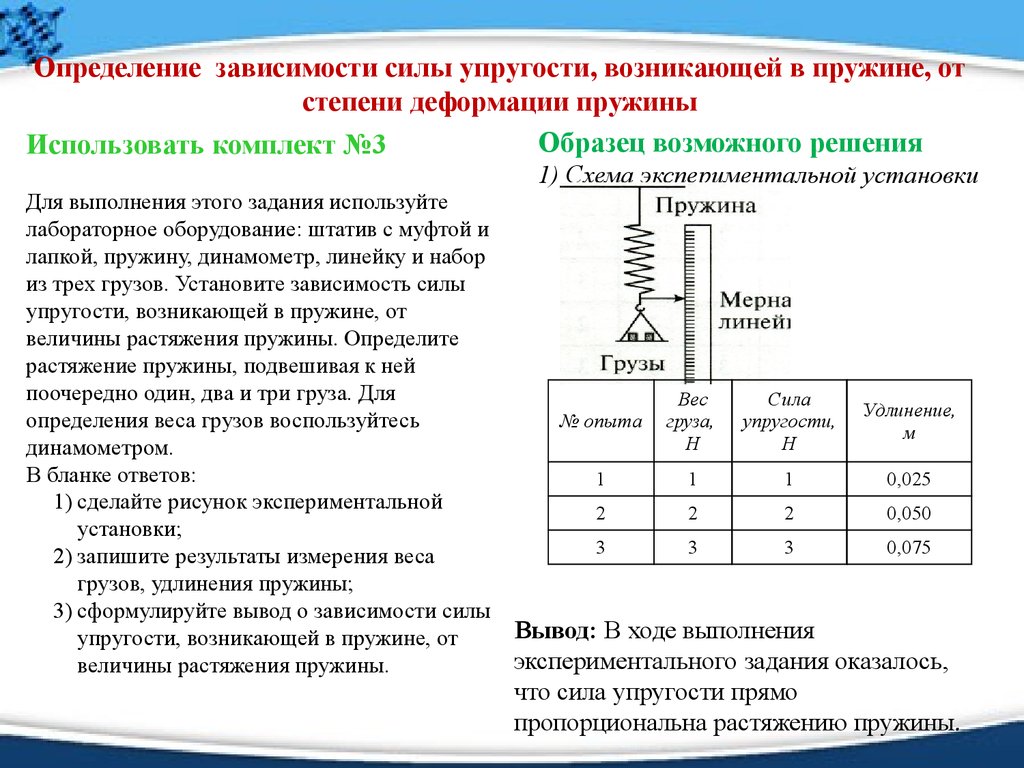 Если построить зависимость напряжения от деформации, то для малых деформаций этот график будет линейным, а наклон линии будет свойством материала, известным как модуль упругости Юнга . Это значение может сильно варьироваться от 1 кПа для желе до 100 ГПа для стали. Для большинства технических материалов линейная область диаграммы напряжения-деформации возникает только при очень малых деформациях (<0,1%). В этом курсе мы сосредоточимся только на материалах, которые линейно-упругие (т. е. они следуют закону Гука) и изотропные  (они ведут себя одинаково независимо от того, в каком направлении вы их тянете).

Из закона Гука и наших определений напряжения и деформации мы можем легко получить простое соотношение для деформации материала.

Интуитивно этот экзамен имеет смысл: приложите больше нагрузки, получите большую деформацию; приложите ту же нагрузку к более жесткому или толстому материалу, получите меньшую деформацию.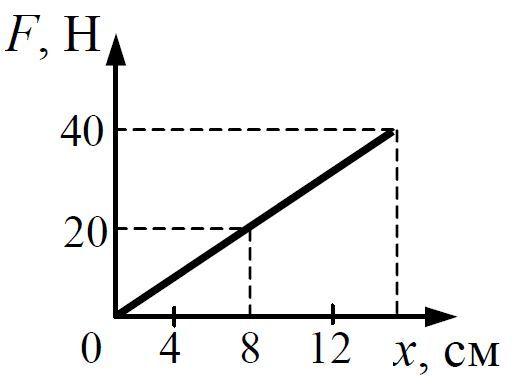 Если конструкция меняет форму или материал или по-разному нагружена в разных точках, мы можем разделить эти множественные нагрузки, используя принцип 9.0015 суперпозиция .

Обобщенный закон Гука

На прошлом уроке мы начали узнавать о том, как связаны стресс и напряжение – через закон Гука. Но до этого момента мы рассматривали только очень упрощенную версию закона Гука: мы говорили только о напряжении или напряжении в одном направлении. В этом уроке мы рассмотрим обобщенный закон Гука для однородных, изотропных и упругих материалов, на которые действуют силы более чем по одной оси.

Прежде всего, даже простое вытягивание (или толкание) большинства материалов в одном направлении на самом деле вызывает деформацию во всех трех ортогональных направлениях . Вернемся к первой иллюстрации напряжения. На этот раз мы учтем тот факт, что вытягивание объекта в осевом направлении приводит к его сжатию в поперечном направлении в поперечном направлении:

Таким образом, потянув за него в направлении x , он сожмется в y  и  z направлений. Это свойство материала известно как коэффициент Пуассона , обозначается греческой буквой nu и определяется как:

Или, более математически, используя осевую нагрузку, показанную на изображении выше, мы можем записать это как уравнение:

Поскольку коэффициент Пуассона представляет собой отношение двух деформаций, а деформация безразмерна, коэффициент Пуассона также безразмерен. Коэффициент Пуассона является материальным свойством . Коэффициент Пуассона может варьироваться от -1 до 0,5. Для большинства инженерных материалов, например стали или алюминия, коэффициент Пуассона составляет около 0,3, а для каучуков коэффициент Пуассона составляет около 0,5, которые называются «несжимаемыми». Несжимаемость просто означает, что на любую величину, которую вы сожмете в одном направлении, она расширится на такую ​​же величину в других направлениях — следовательно, ее объем не изменится.

За последнее десятилетие было проведено очень интересное исследование по созданию структурированных материалов , в которых используются геометрия и упругая нестабильность (тема, которую мы кратко рассмотрим в следующей лекции) для создания ауксетических материалов — материалов с отрицательным коэффициентом Пуассона. Физически это означает, что когда вы тянете материал в одном направлении, он расширяется во всех направлениях (и наоборот):

Этот принцип можно применить и в 3D для создания расширяемых/складных оболочек:

Благодаря коэффициенту Пуассона у нас теперь есть уравнение, связывающее деформацию в направлении y или z с деформацией в направлении z. Мы можем, в свою очередь, связать это обратно со стрессом с помощью закона Гука. Это важное замечание: натяжение объекта в одном направлении вызывает напряжение только в этом направлении , а вызывает напряжение во всех трех направлениях . Итак, сигма _y = sigma _z = 0. Выпишем деформации в y и z относительно напряжения в направлении x .

Помните, что до этого момента мы рассматривали только одноосную деформацию . В действительности конструкции могут быть одновременно нагружены в нескольких направлениях, вызывая напряжение в этих направлениях. Полезный способ понять это — представить очень крошечный «кубик» материала внутри объекта. Этот куб может иметь напряжений , которые являются нормальными к каждой поверхности , например:

Таким образом, приложение нагрузки в направлении x вызывает нормальное напряжение в этом направлении, и то же самое верно для нормальных напряжений в направлениях y и z . И, как мы теперь знаем, напряжение в одном направлении вызывает напряжение во всех трех направлениях . Итак, теперь мы включим эту идею в закон Гука и запишем уравнения для деформации в каждом направлении как:

Эти уравнения выглядят сложнее, чем они есть на самом деле: деформация в каждом направлении (или каждый компонент деформации) зависит от нормального напряжения в этом направлении, а коэффициент Пуассона умножается на деформацию в двух других направлениях. Теперь у нас есть уравнения того, как объект изменит форму в трех ортогональных направлениях. Что ж, если объект меняет форму во всех трех направлениях, значит, он изменит свои том . Простую меру этого изменения объема можно найти, сложив три нормальных компонента деформации:

Теперь, когда у нас есть уравнение для изменения объема, или расширение , в терминах нормальных деформаций, мы можем переписать его в терминах нормальных напряжений.

Очень распространенный тип стресса, который вызывает дилатацию, известен как гидростатический стресс.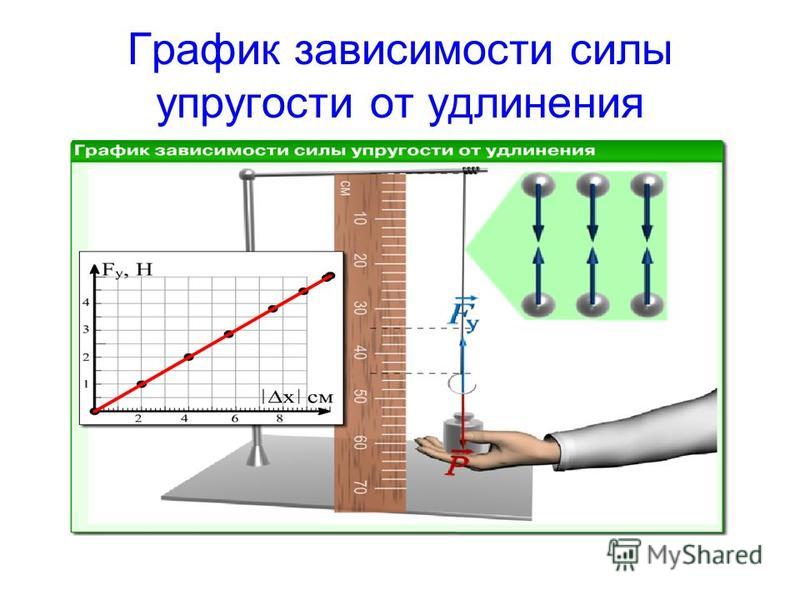 Это просто давление, которое одинаково действует на весь материал. Поскольку он действует одинаково, это означает:

Итак, в случае гидростатического давления мы можем сократить наше окончательное уравнение для расширения до следующего:

Это окончательное соотношение важно, потому что оно определяет, как объем материала изменяется под действием гидростатического давления. Предварительный коэффициент для p можно переписать как объемный модуль материала , K .

Наконец, вернемся к идее «несжимаемых» материалов. Что происходит с K — мерой того, как материал изменяет объем при заданном давлении, — если коэффициент Пуассона для материала равен 0,5?

 

Закон Гука при сдвиге

В предыдущем разделе мы установили связь между нормальным напряжением и нормальной деформацией. Теперь нам нужно поговорить о сдвиге. Вернемся к этому воображаемому кубу материала. В дополнение к внешним силам, вызывающим напряжения, перпендикулярные каждой поверхности куба, силы могут вызывать напряжения, параллельные каждой грани куба.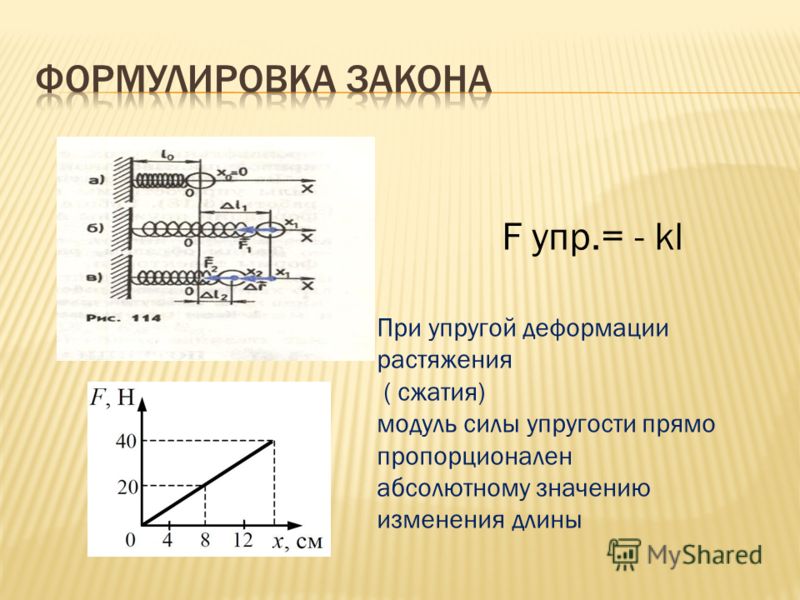 А, как известно, напряжения, параллельные поперечному сечению, равны касательных напряжений

Теперь этот куб материала выглядит намного сложнее, но на самом деле это не так уж и плохо. На каждой поверхности есть два напряжения сдвига, и нижние индексы говорят вам, в каком направлении они указывают и какой поверхности они параллельны. Например, возьмем правую грань куба. Напряжения, перпендикулярные этой грани, являются нормальными напряжениями в направлении x . Есть два напряжения, параллельных этой поверхности, одно указывает в направлении y (обозначается тау _xy ) и одно указывает в направлении z (обозначается тау _хз ). Чтобы куб находился в равновесии, tau _xy = tau _yx (иначе куб вращался бы). Таким образом, теперь имеется шести напряжений (сигма _x , сигма, сигма, тау _xy, тау _yz, тау _xz ), которые характеризуют напряженное состояние в однородном, изотропном, упругом материале.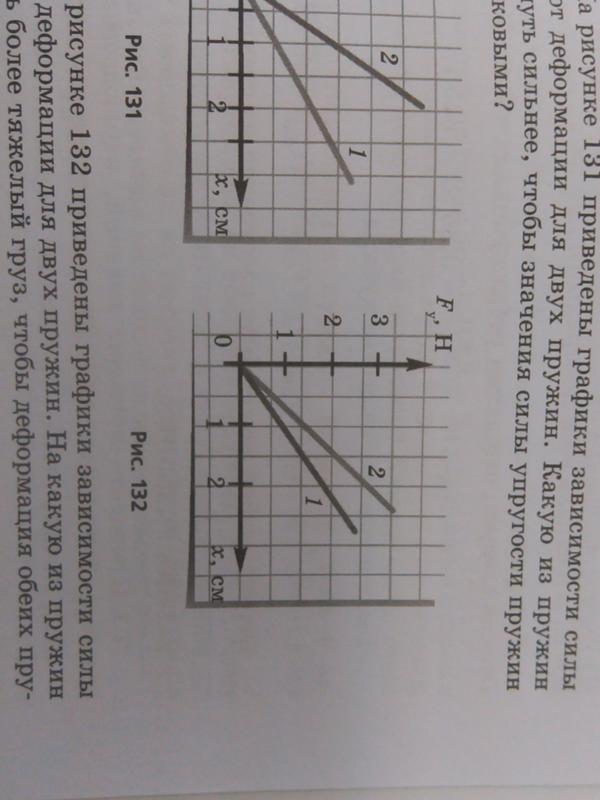

Итак, как эти напряжения сдвига связаны с деформациями сдвига? Закон Гука при сдвиге очень похож на уравнение, которое мы видели для нормального напряжения и деформации:

В этом уравнении пропорция между напряжением сдвига и деформацией сдвига известна как модуль сдвига материала. Это уравнение в его общей форме, но мы можем переписать его более явно с точки зрения компонентов x, y и z . Это даст нам обобщенный закон Гука для однородных изотропных упругих материалов.

В нашем обобщенном законе Гука у нас есть шесть компонентов напряжения и деформации и три свойства материала. Возникает естественный вопрос: как эти три свойства материала соотносятся друг с другом? Это соотношение задается следующим уравнением:

Сводка

В этой лекции мы ввели понятие напряжения. Деформация – это деформация материала от напряжения. Это просто отношение изменения длины к первоначальной длине.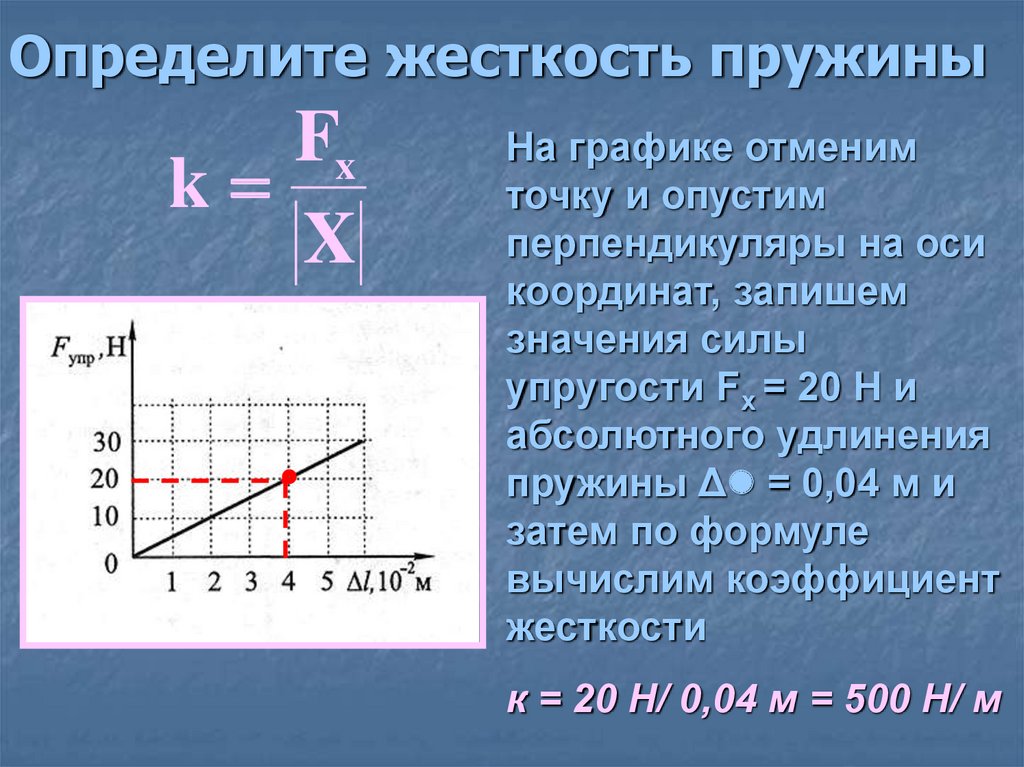 Деформации, прикладываемые перпендикулярно поперечному сечению, представляют собой нормальных деформаций , а деформации, приложенные параллельно поперечному сечению, представляют собой сдвиговых деформаций . Для линейных эластичных материалов напряжение линейно связано с деформацией по закону Гука. Пропорциональность этого отношения известна как материальная модуль упругости . Используя закон Гука, мы можем записать простое уравнение, которое описывает, как материал деформируется под действием внешней нагрузки.

Кроме того, в этом разделе мы узнали о многоосевой нагрузке . В частности, мы узнали, что напряжение в одном направлении вызывает деформацию в трех направлениях . Это происходит из-за свойства материала, известного как коэффициент Пуассона  – отношение между поперечной и осевой деформациями. Деформации, происходящие в трех ортогональных направлениях, могут дать нам меру прочности материала. 0015 расширение  в ответ на многоосевую нагрузку. В частности, объем материала обычно может изменяться в ответ на изменения внешнего давления или гидростатического напряжения . Это привело к определению устойчивости материалов к изменению объема под действием гидростатического напряжения – модуль объемного сжатия . Исследуя воображаемый кубический элемент в произвольном материале, мы смогли представить напряжения, возникающие перпендикулярно и параллельно каждой грани куба. Это дало нам шести напряжений и шесть деформаций (три нормальных и три сдвиговых), которые мы соотнесли друг с другом с помощью обобщенного закона Гука для однородных , изотропных и эластичных материалов. Эти компоненты многоосного напряжения и деформации связаны тремя свойствами материала: модулем упругости Юнга , модулем сдвига и коэффициентом Пуассона .

Этот материал основан на работе, поддержанной Национальным научным фондом в рамках гранта № 1454153. Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национальный научный фонд.

Напряжение и деформация) – x-Douglas College Physics 1107 Fall 2019 Custom учебник

Глава 4 Динамика: сила и законы движения Ньютона

Резюме

• Закон штата Гука.
• Объясните закон Гука, используя графическое изображение между деформацией и приложенной силой.
• Обсудите деформации, такие как изменение длины
• Определите изменение длины, зная массу, длину и радиус.

Силы могут влиять на форму объекта. Если бульдозер втолкнет машину в стену, то машина не сдвинется с места, но заметно изменит форму. Изменение формы под действием силы равно деформация . Известно, что даже очень малые силы вызывают некоторую деформацию. При малых деформациях наблюдаются две важные характеристики. Во-первых, объект возвращается к своей первоначальной форме при снятии силы, то есть деформация является упругой при малых деформациях. Во-вторых, величина деформации пропорциональна силе, т. е. при малых деформациях выполняется закон Гука . В форме уравнения закон Гука имеет вид

.

[латекс]\boldsymbol{F = k\Delta{L},}[/латекс]

, где Δ L — величина деформации (например, изменение длины), вызванная силой F , а k — константа пропорциональности, которая зависит от формы и состава объект и направление силы. Обратите внимание, что эта сила является функцией деформации Δ L — она не постоянна, как кинетическая сила трения. Иногда мы используем Δ x  вместо Δ L.  Деформация может быть по любой оси. Переставить это на

[латекс]\boldsymbol{\Delta{L}\: = }[/латекс][латекс]\boldsymbol{\frac{F}{k}}[/латекс]

дает понять, что деформация пропорциональна приложенной силе.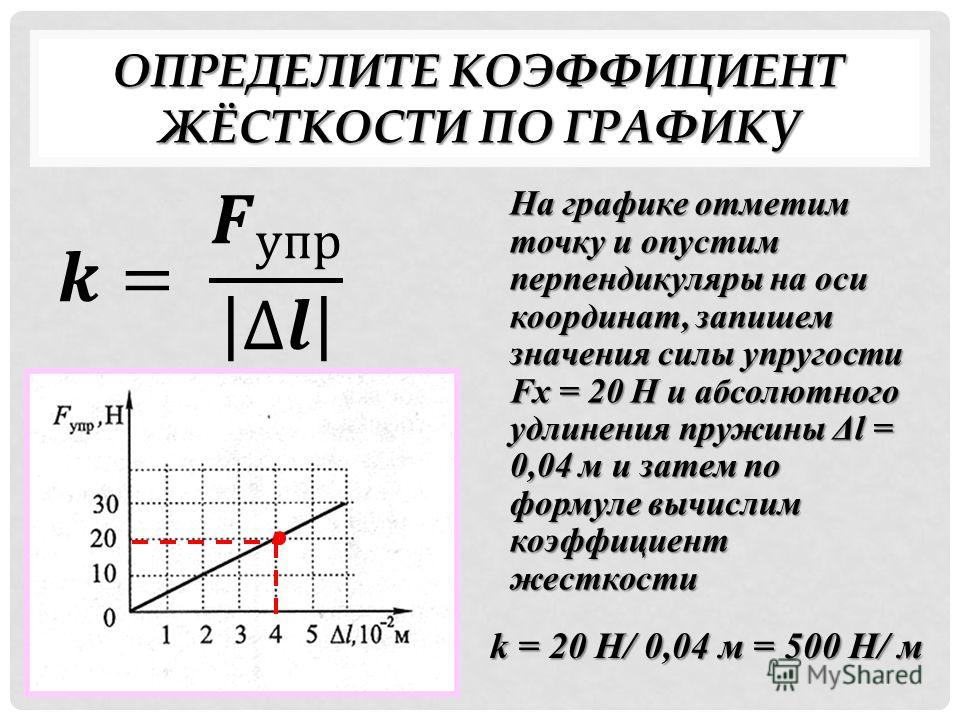 На рис. 1 показана зависимость по закону Гука между протяженностью Δ L пружины или кости человека. Для металлов или пружин прямолинейная область, к которой относится закон Гука, намного больше. Кости хрупкие, эластичная область мала, а перелом внезапный. В конце концов, достаточно большое напряжение на материале приведет к его разрыву или разрушению. Прочность на растяжение — это разрушающее напряжение, вызывающее необратимую деформацию или разрушение материала.

ЗАКОН ГУКА

[латекс]\boldsymbol{F = k\Delta{L},}[/латекс]

где Δ L — величина деформации (например, изменение длины), вызванная сила F и k является константой пропорциональности, которая зависит от формы и состава объекта и направления силы.

[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{F}{k}}[/латекс]

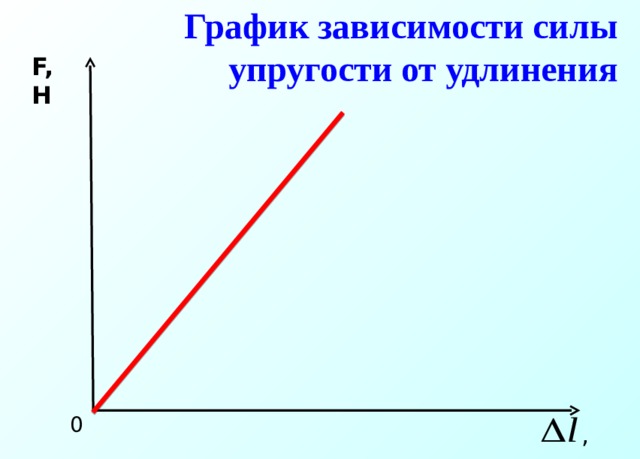
Рисунок 1. График деформации Δ L в зависимости от приложенной силы F . Прямой отрезок — это линейный участок, на котором соблюдается закон Гука. Наклон прямой области равен 1 / k . Для больших сил график искривлен, но деформация остается упругой — Δ L вернется к нулю, если усилие будет устранено. Еще большие силы постоянно деформируют объект, пока он окончательно не сломается. Форма кривой вблизи разрушения зависит от нескольких факторов, в том числе от того, как сила F . Обратите внимание, что на этом графике наклон увеличивается непосредственно перед переломом, указывая на то, что небольшое увеличение F приводит к большому увеличению L вблизи перелома.

Константа пропорциональности k зависит от ряда факторов для материала. Например, гитарная струна из нейлона растягивается при натяжении, и удлинение Δ L пропорционально приложенной силе (по крайней мере, при малых деформациях).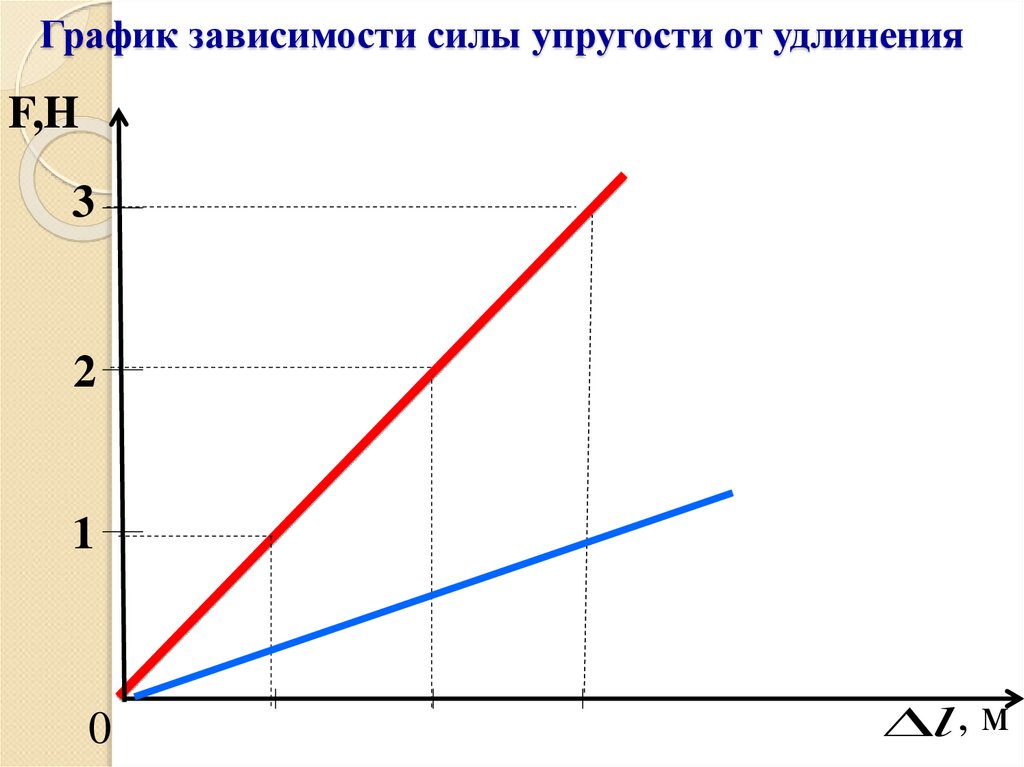 Более толстые нейлоновые струны и те, что сделаны из стали, меньше растягиваются при одном и том же приложенном усилии, что означает, что они имеют большее 9-кратное усилие.0097 k (см. рис. 2). Наконец, все три струны возвращаются к своей нормальной длине после снятия силы при условии, что деформация невелика. Большинство материалов ведет себя таким образом, если деформация составляет менее примерно 0,1% или примерно 1 часть на 10 ³ .

Рисунок 2. Одна и та же сила, в данном случае вес ( w ), приложенная к трем разным гитарным струнам одинаковой длины, вызывает три разные деформации, показанные заштрихованными сегментами. Струна слева из тонкого нейлона, та, что посередине, из нейлона потолще, а та, что справа, из стали.

НЕМНОГО ПОТЯНИТЕСЬ

Как бы вы измерили константу пропорциональности k резиновой ленты? Если резиновая лента растянулась на 3 см, когда к ней прикреплен груз массой 100 г, то насколько сильно она растянется, если две одинаковые резиновые ленты будут прикреплены к одной и той же массе, даже если их сложить параллельно или, наоборот, связать вместе последовательно?

 

 

Решения

Задачи и упражнения

1) 110 Н/м

2) 0,0101 м = 1,01 см

3) 1,11 ньютона

4) 6,0 см       По отношению и пропорции      12 Н/4,0 см = 18 Н/4,0 см? так ? = 18 х 4 / 12 =

 

 

Теперь рассмотрим тип деформации, вызывающий изменение длины (растяжение и сжатие).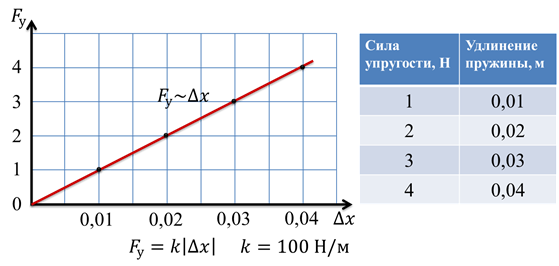 Существуют также боковые силы, вызывающие сдвиг (напряжение) и изменение объема, но мы не будем подробно останавливаться на них в этом курсе.

Изменение длины Δ L получается, когда к проволоке или стержню прикладывают силу, параллельную его длине L ₀ , либо растягивая его (растяжение), либо сжимая его. (См. рис. 3.)

Рисунок 3. (а) Натяжение. Стержень растянут на длину Δ L , когда сила приложена параллельно его длине. (б) Сжатие. Тот же стержень сжимается силами одинаковой величины в противоположном направлении. Для очень малых деформаций и однородных материалов Δ L примерно одинаково для одной и той же величины растяжения или сжатия. При больших деформациях площадь поперечного сечения изменяется при сжатии или растяжении стержня.

Эксперименты показали, что изменение длины ( Δ L ) зависит лишь от нескольких переменных.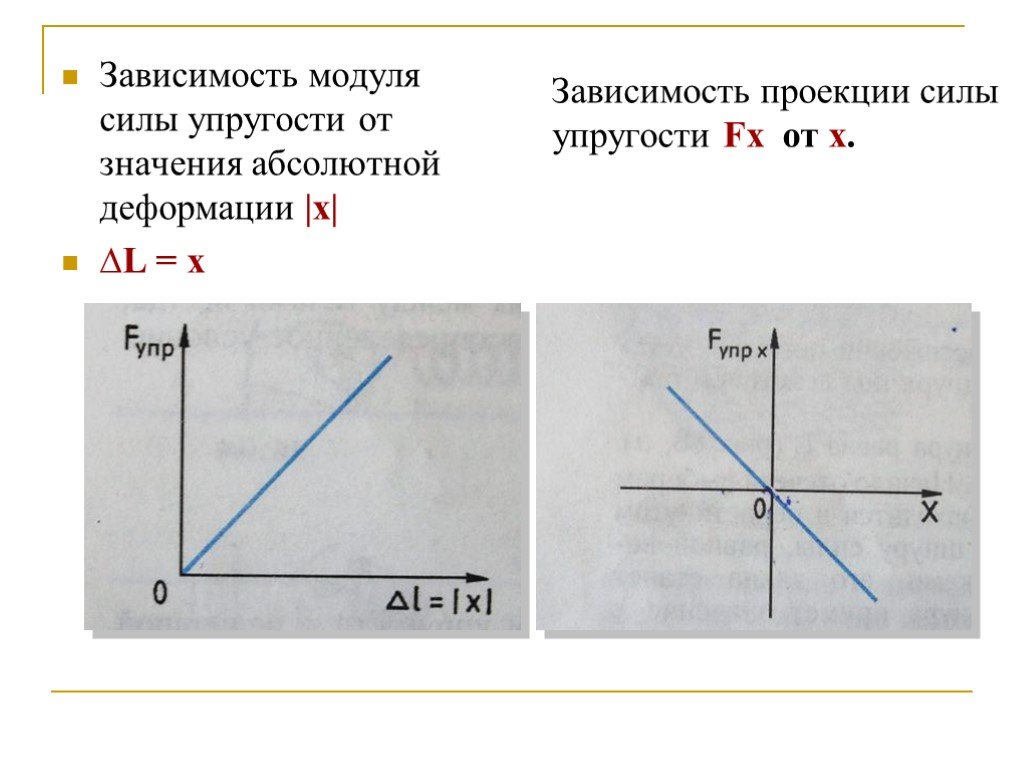 Как уже отмечалось, Δ L пропорционально силе F и зависит от вещества, из которого сделан предмет. Кроме того, изменение длины пропорционально исходной длине L ₀ и обратно пропорциональна площади поперечного сечения проволоки или стержня. Например, длинная гитарная струна растянется больше, чем короткая, а толстая струна растянется меньше, чем тонкая. Мы можем объединить все эти факторы в одно уравнение для Δ L :

[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{1}{Y}\frac{\vec{\textbf{F}}}{A} }[/латекс][латекс]\boldsymbol{L_0},[/латекс]

где Δ L изменение длины, F приложенная сила, Y коэффициент, называемый модулем упругости или модулем Юнга, который зависит от вещества,

A 5 площадь поперечного сечения, а L ₀ — исходная длина. В таблице 3 приведены значения Y для нескольких материалов. Говорят, что материалы с большим значением Y имеют большую жесткость при растяжении, поскольку они меньше деформируются при заданном растяжении или сжатии. 92)}[/латекс] Алюминий 70 25 75 Кость – растяжение 16 80 8 Кость – сжатие 9 Латунь 90 35 75 Кирпич 15 Бетон 20 Стекло 70 20 30 Гранит 45 20 45 Волосы (человеческие) 10 Твердая древесина 15 10 Чугун, литой 100 40 90 Свинец 16 5 50 Мрамор 60 20 70 Нейлон 5 Полистирол 3 Шелк 6 Паутинная резьба 3 Сталь 210 80 130 Сухожилие 1 Ацетон 0,7 Этанол 0,9 Глицерин 4,5 Меркурий 25 Вода 2,2 Таблица 3. Модули упругости ¹ .

Модули Юнга для жидкостей и газов не указаны в таблице 3, поскольку они не могут растягиваться или сжиматься только в одном направлении. Обратите внимание, что существует предположение, что объект не ускоряется, так что на самом деле есть две приложенные силы величиной F действуют в противоположных направлениях. Например, струны на Рисунке 3 тянут вниз силой величины w и удерживаются потолком, который также оказывает силу величиной w .

Пример 1: натяжение длинного троса

Подвесные тросы используются для перевозки гондол на горнолыжных курортах. (См. рис. 4) Рассмотрим подвесной трос с неподдерживаемым пролетом длиной 3 км. Рассчитайте величину растяжения стального троса. Предположим, что кабель имеет диаметр 5,6 см и максимальное натяжение, которое он может выдержать, равно 3,0 × 10 ⁶ Н .

Рис. 4. Гондолы перемещаются по подвесным тросам на горнолыжном курорте Гала Юдзава в Японии. (кредит: Руди Герман, Flickr)

Стратегия

Сила равна максимальному натяжению, или F = 3,0 × 10 ⁶ Н . Площадь поперечного сечения π r ² = 2,46 × 10 ^-3 м ² . Уравнение [латекс]\жирныйсимвол{\Delta{L} = \frac{1}{Y}\frac{F}{A}L_0}[/latex] можно использовать для определения изменения длины. 92})(3020\textbf{ m})}[/latex]

[latex]\boldsymbol{=18\textbf{ m}}.[/latex]

Обсуждение

Это довольно натянуто, но только около 0,6% длины без поддержки. Влияние температуры на длину может быть важным в этих условиях.

Кости в целом не ломаются при растяжении или сжатии. Скорее, они обычно ломаются из-за бокового удара или изгиба, что приводит к сдвигу или хрусту кости. Поведение костей при растяжении и сжатии важно, поскольку оно определяет нагрузку, которую кости могут нести. Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревьях. Несущие конструкции имеют особенности; колонны в здании имеют стальные арматурные стержни, а деревья и кости — волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости располагается тонкими пластинками, разделенными костным мозгом, тогда как в других местах кости могут быть цилиндрическими и наполненными костным мозгом или просто сплошными. Люди с избыточным весом склонны к повреждению костей из-за постоянного сжатия в суставах и сухожилиях.

Другой биологический пример закона Гука происходит в сухожилиях. Функционально сухожилие (ткань, соединяющая мышцу с костью) должно сначала легко растягиваться при приложении силы, но обеспечивать гораздо большую восстанавливающую силу при большем напряжении. На рис. 5 показана зависимость между напряжением и деформацией сухожилия человека. Некоторые сухожилия имеют высокое содержание коллагена, поэтому напряжение или изменение длины относительно невелики; другие, такие как опорные сухожилия (как в ноге), могут изменять длину до 10%. Обратите внимание, что эта кривая напряжения-деформации нелинейна, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальцев, волокна сухожилия начинают выстраиваться в направлении напряжения — это называется 9.0097 разжим . В линейной области фибриллы будут растягиваться, а в области разрушения отдельные волокна начинают рваться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения. Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.

Рисунок 5. Типичная кривая напряжения-деформации для сухожилий млекопитающих. Показаны три области: (1) область носка (2) линейная область и (3) область отказа.

В отличие от костей и сухожилий, которые должны быть прочными и эластичными, артерии и легкие должны быть очень растяжимыми. Эластические свойства артерий необходимы для кровотока. Давление в артериях увеличивается, и стенки артерий растягиваются, когда кровь выталкивается из сердца. Когда аортальный клапан закрывается, давление в артериях падает, и стенки артерий расслабляются, чтобы поддерживать кровоток. Когда вы чувствуете свой пульс, вы чувствуете именно это — эластичное поведение артерий по мере того, как кровь течет через них при каждом толчке сердца. Если бы артерии были жесткими, вы бы не почувствовали пульс. Сердце также является органом с особыми эластическими свойствами. Легкие расширяются за счет мышечного усилия, когда мы вдыхаем, но свободно и эластично расслабляются, когда мы выдыхаем. Наша кожа особенно эластична, особенно у молодых. Молодой человек может похудеть со 100 кг до 60 кг без видимых провисаний кожи. Эластичность всех органов с возрастом снижается. Постепенное физиологическое старение за счет снижения эластичности начинается в начале 20-летнего возраста.

Пример 2. Расчет деформации: насколько укорачивается ваша нога, когда вы стоите на ней?

Рассчитайте изменение длины бедренной кости голени, когда мужчина массой 70,0 кг поддерживает на ней 62,0 кг своего веса, предполагая, что кость эквивалентна однородному стержню длиной 40,0 см и радиусом 2,00 см . 2) = 607.6\textbf{N}},[/латекс]

, а площадь поперечного сечения равна π r ² = 1,257 × 10 ^-3 м ² . Уравнение [латекс]\жирныйсимвол{\Delta{L} = \frac{1}{Y}\frac{F}{A}L_0}[/latex] можно использовать для определения изменения длины.

Раствор

Все количества, кроме Δ L , известны. Обратите внимание, что здесь необходимо использовать значение сжатия для модуля Юнга кости. Таким образом,

[латекс]\boldsymbol{\Delta{L}=(\frac{1}{9{-5}\textbf{ м}}.[/latex]

Обсуждение

Это небольшое изменение длины кажется разумным, согласующимся с нашим опытом, что кости жесткие. На самом деле, даже довольно большие силы, возникающие при напряженной физической работе, не сильно сжимают или сгибают кости. Хотя кость жесткая по сравнению с жиром или мышцами, некоторые из веществ, перечисленных в таблице 3, имеют более высокие значения модуля Юнга Y . Другими словами, они более жесткие.

Уравнение изменения длины традиционно перестраивается и записывается в следующем виде:

[латекс]\boldsymbol{\frac{F}{A}}[/latex][латекс]\boldsymbol{=Y}[/латекс][латекс]\boldsymbol{\frac{\Delta{L}}{L_0 }}.[/латекс]

Отношение силы к площади, [латекс]\boldsymbol{\frac{F}{A}},[/латекс]  определяется как напряжение (измеряется в Н/м ² ), а отношение изменения длины в длину,[латекс]\жирныйсимвол{\гидроразрыва{\Delta{L}}{L_0}},[/латекс]определяется как штамм (безразмерное количество). Другими словами,

[латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]

В этой форме уравнение аналогично закону Гука, где напряжение аналогично силе, а деформация аналогична деформации. Если мы снова перепишем это уравнение к виду

[латекс]\boldsymbol{F=YA}[/латекс][латекс]\boldsymbol{\frac{\Delta{L}}{L_0}},[/latex]

видим, что это то же самое, что и закон Гука с константой пропорциональности

[латекс]\boldsymbol{k\:=}[/латекс][латекс]\boldsymbol{\frac{YA}{L_0}}. [/latex]

Эта общая идея о том, что сила и вызываемая ею деформация пропорциональны малым деформациям, применима к изменениям длины, боковому изгибу и изменениям объема.

НАПРЯЖЕНИЕ

Отношение силы к площади [латекс]\boldsymbol{\frac{F}{A}},[/латекс] определяется как напряжение, измеренное в Н/м ² .

НАПРЯЖЕНИЕ

Отношение изменения длины к длине [латекс]\boldsymbol{\frac{\Delta{L}}{L_0}},[/латекс] определяется как напряжение (безразмерная величина). Другими словами,

[латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]

• Закон Гука определяется выражением

  [латекс]\boldsymbol{F=k\Delta{L}},[/latex]    или  [латекс]\boldsymbol{F=k\Delta{x}},[/latex]

  , где Δ L — величина деформации (изменение длины), F — приложенная сила, а k — константа пропорциональности, зависящая от формы и состава объекта. и направление силы. Связь между деформацией и приложенной силой также можно записать как

  [латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{1}{Y}\frac{F}{A}}[/latex][латекс] \boldsymbol{L_0},[/латекс]

  , где Y — это модуль Юнга , зависящий от вещества, A — площадь поперечного сечения, а L ₀ — исходная длина.

• Отношение силы к площади [латекс]\boldsymbol{\frac{F}{A}},[/латекс] определяется как напряжение , измеренное в Н/м ² .
• Отношение изменения длины к длине [латекс]\boldsymbol{\frac{\Delta{L}}{L_0}},[/латекс] определяется как штамм (безразмерная величина). Другими словами,

  [латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]

Сноски

1. 1 Приблизительные и средние значения. Модули Юнга Y для растяжения и сжатия иногда различаются, но здесь они усреднены.