Содержание
Закон Ома — формулировка простыми словами, определение
Покажем, как применять знание физики в жизни
Начать учиться
180.9K
Резистор — смелый элемент, потому что умудряется противостоять хитрому и умному электрическому току. О том, почему ток вдруг хитрый, и как все величины электрической цепи взаимосвязаны — в этой статье.
Сопротивление
Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.
Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.
Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.
Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.
Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.
Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.
Эту закономерность можно описать следующей формулой:
|
Сопротивление R = ρ · l/S R — сопротивление [Ом] l — длина проводника [м] S — площадь поперечного сечения [мм2] ρ — удельное сопротивление [Ом · мм2/м] |
Единица измерения сопротивления — ом.
Будьте внимательны!
Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм2. При умножении мм2 сокращаются и мы получаем величину в СИ.
Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм2.
Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Таблица удельных сопротивлений различных материалов
|
Материал |
Удельное сопротивление ρ, Ом · мм2/м |
|
Алюминий |
0,028 |
|
Бронза |
0,095–0,1 |
|
Висмут |
1,2 |
|
Вольфрам |
0,05 |
|
Железо |
0,1 |
|
Золото |
0,023 |
|
Иридий |
0,0474 |
|
Константан (сплав NiCu + Mn) |
0,5 |
|
Латунь |
0,025–0,108 |
|
Магний |
0,045 |
|
Манганин (сплав меди марганца и никеля — приборный) |
0,43–0,51 |
|
Медь |
0,0175 |
|
Молибден |
0,059 |
|
Нейзильбер (сплав меди, цинка и никеля) |
0,2 |
|
Натрий |
0,047 |
|
Никелин (сплав меди и никеля) |
0,42 |
|
Никель |
0,087 |
|
Нихром (сплав никеля, хрома, железа и марганца) |
1,05–1,4 |
|
Олово |
0,12 |
|
Платина |
0,107 |
|
Ртуть |
0,94 |
|
Свинец |
0,22 |
|
Серебро |
0,015 |
|
Сталь |
0,103–0,137 |
|
Титан |
0,6 |
|
Хромаль |
1,3–1,5 |
|
Цинк |
0,054 |
|
Чугун |
0,5–1,0 |
Резистор
Все реальные проводники имеют сопротивление, но его стараются сделать незначительным.
Из-за того, что проводник у нас «кругом-бегом-такой-идеальный», чаще всего за сопротивление в цепи отвечает резистор. Это устройство, которое нагружает цепь сопротивлением.
Вот так резистор изображается на схемах:
В школьном курсе физики используют европейское обозначение, поэтому запоминаем только его. Американское обозначение можно встретить, например, в программе Micro-Cap, в которой инженеры моделируют схемы.
Вот так резистор выглядит в естественной среде обитания:
Полосочки на нем показывают его сопротивление.
На сайте компании Ekits, которая занимается продажей электронных модулей, можно выбрать цвет резистора и узнать значение его сопротивления:
Источник: сайт компании Ekits
О том, зачем дополнительно нагружать сопротивлением цепь, мы поговорим в этой же статье чуть позже.
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.
Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
|
Сопротивление R = ρ · l/S R — сопротивление [Ом] l — длина проводника [м] S — площадь поперечного сечения [мм2] ρ — удельное сопротивление [Ом · мм2/м] |
Закон Ома для участка цепи
С камушками в трубе все понятно, но не только же от них зависит сила, с которой поток воды идет по трубе — от насоса, которым мы эту воду качаем, тоже зависит.
Например, источником может быть гальванический элемент (привычная батарейка). Батарейка работает на основе химических реакций внутри нее. В результате этих реакций выделяется энергия, которая потом передается электрической цепи.
У любого источника обязательно есть полюса — «плюс» и «минус». Полюса — это его крайние положения, по сути клеммы, к которым присоединяется электрическая цепь. Собственно, ток как раз течет от «+» к «−».
У нас уже есть две величины, от которых зависит электрический ток в цепи — напряжение и сопротивление. Кажется, пора объединять их в закон.
Сила тока в участке цепи прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.
Математически его можно описать вот так:
|
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Напряжение измеряется в Вольтах и показывает разницу между двумя точками цепи: от этой разницы зависит, насколько сильно будет течь ток — чем больше разница, тем выше напряжение и ток будет течь сильнее.
Сила тока измеряется в амперах, а подробнее о ней вы можете прочитать в нашей статье. 😇
Давайте решим несколько задач на закон Ома для участка цепи.
Задача раз
Найти силу тока в лампочке накаливания торшера, если его включили в сеть напряжением 220 В, а сопротивление нити накаливания равно 880 Ом.
Решение:
Возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/880 = 0,25 А
Ответ: сила тока, проходящего через лампочку, равна 0,25 А
Давайте усложним задачу. И найдем силу тока, зная все параметры для вычисления сопротивления и напряжение.
Задача два
Найти силу тока в лампочке накаливания, если торшер включили в сеть напряжением 220 В, а длина нити накаливания равна 0,5 м, площадь поперечного сечения 0,01 мм2, а удельное сопротивление нити равно 1,05 Ом · мм2/м.
Решение:
Сначала найдем сопротивление проводника.
R = ρ · l/S
Площадь дана в мм2, а удельное сопротивления тоже содержит мм2 в размерности.
Это значит, что все величины уже даны в СИ и перевод не требуется:
R = 1,05 · 0,5/0,01 = 52,5 Ом
Теперь возьмем закон Ома для участка цепи:
I = U/R
Подставим значения:
I = 220/52,5 ≃ 4,2 А
Ответ: сила тока, проходящего через лампочку, приблизительно равна 4,2 А
А теперь совсем усложним! Определим материал, из которого изготовлена нить накаливания.
Задача три
Из какого материала изготовлена нить накаливания лампочки, если настольная лампа включена в сеть напряжением 220 В, длина нити равна 0,5 м, площадь ее поперечного сечения равна 0,01 мм2, а сила тока в цепи — 8,8 А
Решение:
Возьмем закон Ома для участка цепи и выразим из него сопротивление:
I = U/R
R = U/I
Подставим значения и найдем сопротивление нити:
R = 220/8,8 = 25 Ом
Теперь возьмем формулу сопротивления и выразим из нее удельное сопротивление материала:
R = ρ · l/S
ρ = RS/l
Подставим значения и получим:
ρ = 25 · 0,01/0,5 = 0,5 Ом · мм2/м
Обратимся к таблице удельных сопротивлений материалов, чтобы выяснить, из какого материала сделана эта нить накаливания.
Ответ: нить накаливания сделана из константана.
Закон Ома для полной цепи
Мы разобрались с законом Ома для участка цепи. А теперь давайте узнаем, что происходит, если цепь полная: у нее есть источник, проводники, резисторы и другие элементы.
В таком случае вводится закон Ома для полной цепи: сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Так, стоп. Слишком много незнакомых слов — разбираемся по порядку.
Что такое ЭДС и откуда она берется
ЭДС расшифровывается, как электродвижущая сила. Обозначается греческой буквой ε и измеряется, как и напряжение, в Вольтах.
ЭДС — это сила, которая движет заряженные частицы в цепи. Она берется из источника тока. Например, из батарейки.
Химическая реакция внутри гальванического элемента (это синоним батарейки) происходит с выделением энергии в электрическую цепь.
Зачастую напряжение и ЭДС приравнивают и говорят, что это одно и то же. Формально, это не так, но при решении задач чаще всего и правда нет разницы, так как эти величины обе измеряются в Вольтах и определяют очень похожие по сути своей процессы.
В виде формулы Закон Ома для полной цепи будет выглядеть следующим образом:
|
Закон Ома для полной цепи I — сила тока [A] ε — ЭДС [В] R — сопротивление нагрузки [Ом] r — внутреннее сопротивление источника [Ом] |
Любой источник не идеален.
Решим задачу на полную цепь.
Задачка
Найти силу тока в полной цепи, состоящей из одного резистора сопротивлением 3 Ом и источником с ЭДС равной 4 В и внутренним сопротивлением 1 Ом
Решение:
Возьмем закон Ома для полной цепи:
Подставим значения:
A
Ответ: сила тока в цепи равна 1 А.
Когда «сопротивление бесполезно»
Электрический ток — умный и хитрый парень. Если у него есть возможность обойти резистор и пойти по идеальному проводнику без сопротивления, он это сделает.
А вот на рисунке ниже сопротивление цепи равно нулю, потому что ток через резистор не пойдет.
Ток идет по пути наименьшего сопротивления.
Теперь давайте посмотрим на закон Ома для участка цепи еще раз.
|
Закон Ома для участка цепи I = U/R I — сила тока [A] U — напряжение [В] R — сопротивление [Ом] |
Подставим сопротивление, равное 0.
То есть:
I = U/0 = ∞
Такой случай называют коротким замыканием — когда величина силы тока настолько велика, что можно устремить ее к бесконечности. В таких ситуациях мы видим искру, бурю, безумие — и все ломается.
Это происходит, потому что две точки цепи имеют между собой напряжение (то есть между ними есть разница). Это как если вдоль реки неожиданно появляется водопад. Из-за этой разницы возникает искра, которую можно избежать, поставив в цепь резистор.
Именно во избежание коротких замыканий нужно дополнительное сопротивление в цепи.
Параллельное и последовательное соединение
Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.
|
Последовательное соединение |
Параллельное соединение |
|
|
Схема |
Резисторы следуют друг за другом
|
Между резисторами есть два узла
Узел — это соединение трех и более проводников |
|
Сила тока |
Сила тока одинакова на всех резисторах I = I1 = I2 |
Сила тока, входящего в узел, равна сумме сил токов, выходящих из него I = I1 + I2 |
|
Напряжение |
Общее напряжение цепи складывается из напряжений на каждом резисторе U = U1 + U2 |
Напряжение одинаково на всех резисторах U = U1 = U2 |
|
Сопротивление |
Общее сопротивление цепи складывается из сопротивлений каждого резистора R = R1 + R2 |
Общее сопротивление для бесконечного количества параллельно соединенных резисторов 1/R = 1/R1 + 1/R2 + … + 1/Rn Общее сопротивление для двух параллельно соединенных резисторов Общее сопротивление бесконечного количества параллельно соединенных одинаковых резисторов R = R1/n |
Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала?
Начнем с того, что все электронные компоненты изготавливаются по ГОСТу.
Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой.
Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного.
Решим несколько задач на последовательное и параллельное соединение.
Задачка раз
Найти общее сопротивление цепи.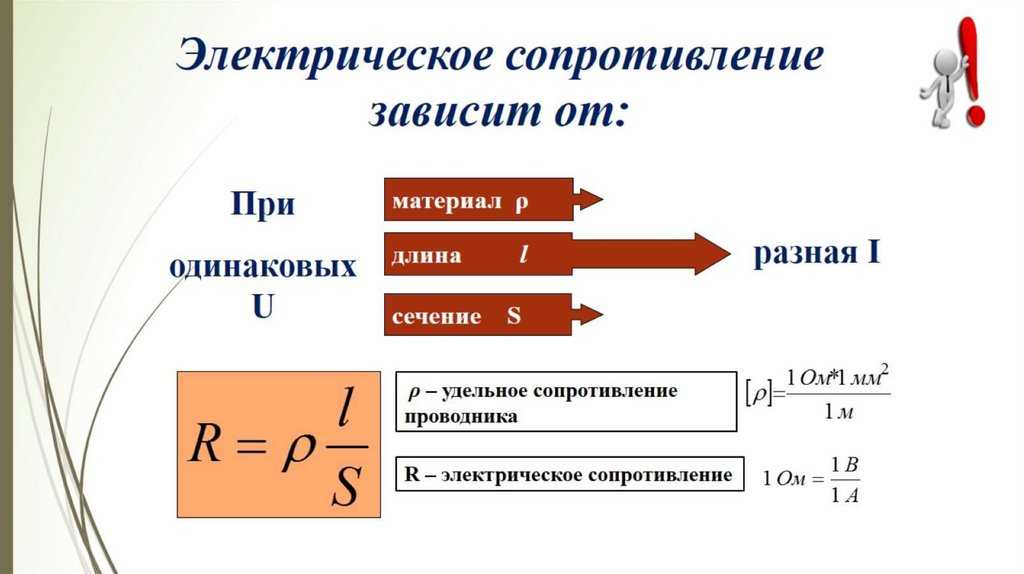
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.
Решение:
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом
Ответ: общее сопротивление цепи равно 10 Ом
Задачка два
Найти общее сопротивление цепи.
R1 = 4 Ом, R2 = 2 Ом
Решение:
Общее сопротивление при параллельном соединении рассчитывается по формуле:
Ом
Ответ: общее сопротивление цепи равно Ом
Задачка три
Найти общее сопротивление цепи, состоящей из резистора и двух ламп.
R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом
Решение:
Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.
В данном случае соединение является смешанным. Лампы соединены параллельно, а последовательно к ним подключен резистор.
Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:
Ом
Общее сопротивление при последовательном соединении рассчитывается по формуле:
R = R1 + Rламп = 1 + 1,2 = 2,2 Ом
Ответ: общее сопротивление цепи равно 2,2 Ом.
Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи 💪.
Задачка четыре со звездочкой
К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.
Решение:
Найдем сначала сопротивление лампы.
Rлампы = R/2 = 10/2 = 5 Ом
Теперь найдем общее сопротивление двух параллельно соединенных резисторов.
Ом
И общее сопротивление цепи равно:
R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом
Выразим внутреннее сопротивление источника из закона Ома для полной цепи.
R + r = ε/I
r = ε/I − R
Подставим значения:
r = 12/0,5 − 10 = 14 Ом
Ответ: внутреннее сопротивление источника равно 14 Ом.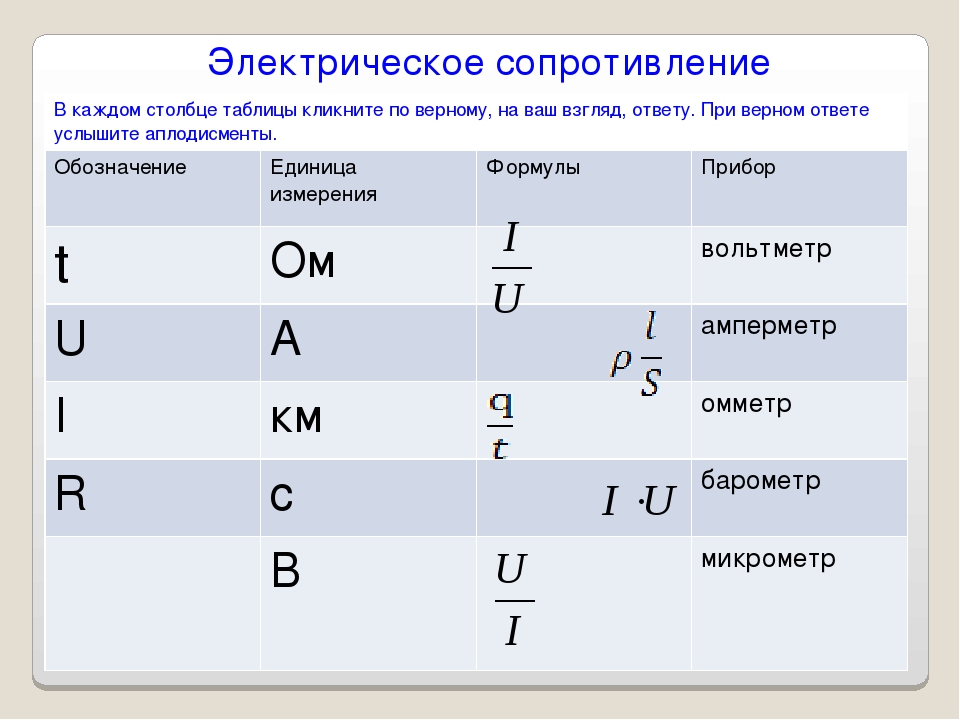
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Карина Хачатурян
К предыдущей статье
128.3K
Коэффициент полезного действия (КПД)
К следующей статье
Сила тока
Получите индивидуальный план обучения физике на бесплатном вводном уроке
На вводном уроке с методистом
-
Выявим пробелы в знаниях и дадим советы по обучению
-
Расскажем, как проходят занятия
-
Подберём курс
что это такое, формула, как измерять
Электрическое сопротивление характеризует свойство проводника оказывать противодействие направленному движению заряженных частиц.
Влияние электрического сопротивления на электрический ток можно представить следующим образом:
- Движение свободных носителей электрического заряда внутри проводника приводит к тому, что свободные носители заряда сталкиваются с атомами и нарушают их поток.
- Этот эффект называется сопротивлением, которое обладает свойством ограничивать электрический ток в электрической цепи.
- Столкновение носителей электрического заряда с атомами также имеет тепловой эффект. Соответствующий элемент электрической цепи становится теплым или даже горячим. Если он перегреется, он может выйти из строя.
Электрическое сопротивление говорит о том, какое напряжение U необходимо, чтобы заставить электрический ток определенной силы тока I протекать через проводник. В физике для обозначения электрического сопротивления в формуле используется прописная буква R (от английского слова «Resistor» или «Resistance»).
Аналогия с потоком воды
Когда речь идет об электрическом сопротивлении в физике, необходимо различать два случая:
- Электрические сопротивления как элементы электрической цепи (см. пример на рисунке 2). То есть, если вы называете элемент в электротехнике резистором, то вы имеете в виду конкретный элемент, предназначенный для целей ограничения протекания электрического тока в электрической цепи.
- Электрическое сопротивление как физическая величина. Вы также можете спросить, насколько сильно тот или иной элемент препятствует протеканию электрического тока или вообще как можно рассчитать электрическое сопротивление. Здесь вы говорите об электрическом сопротивлении как о физической величине.
Примечание. Резистор — это прибор с постоянным сопротивлением. Если необходимо регулировать силу тока в электрической цепи, то используют для этой цели реостаты — приборы с переменным сопротивлением. В составе реостата имеется подвижный контакт, при помощи которого изменяется длина участка, включённого в цепь. Реостат используется, например, в регуляторах громкости радиоприёмников.
Вы можете проиллюстрировать работу резистора как элемента (т.е. случай 1) с помощью модели протекания воды в трубе.
Если представить поток электрического тока как поток воды через трубу, то резистор, имеющий электрическое сопротивление R, выполняет функцию сужения трубы.
Рис. 1. Суть электрического сопротивления на примере модели протекания воды в трубе
Формулы для определения электрического сопротивления
Согласно закона Ома для участка электрической цепи следует, что если вы измеряете напряжение U на проводнике и через него течет ток силой I, то проводник имеет электрическое сопротивление R, равное U, деленное на I, т.е. R = U / I. Единицей измерения электрического сопротивления в СИ является Ом, которая названа в честь немецкого физика Георга Симона Ома. То есть, 1 Ом — это сопротивление проводника, в котором при напряжении 1 В проходит ток силой 1 А. Поэтому, иногда, электрическое сопротивление ещё могут называть «омическим сопротивлением».
Рис. 2. Определение электрического сопротивления
Для очень малых или очень больших сопротивлений используются такие дополнения, как милли-, кило- или мегаом.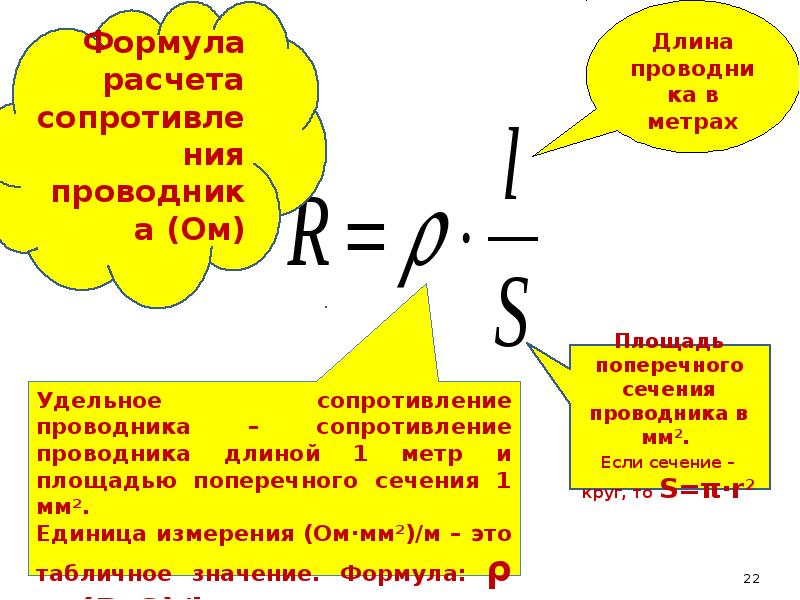
- 1 Миллиом = 1 мОм = 1*10-3 Ом;
- 1 Килоом = 1 кОм = 1*103 Ом;
- 1 Мегаом = 1 МОм = 1*106 Ом.
Интересный факт! Электрическое сопротивление человеческого тела может изменяться от 20000 Ом до 1800 Ом.
Также вы можете рассчитать электрическое сопротивление проводников с помощью их геометрических характеристик. Формула для этого следующая (см. также рисунок 3):
R = (ρ * l) / S, где
- R — электрическое сопротивление проводника;
- l — длина проводника;
- S — площадь поперечного сечения проводника;
- ρ — удельное сопротивление вещества проводника (выбирается по таблицам).
Рис. 3. Электрическое сопротивление проводника
Другими словами, чем тоньше и длиннее проводник, тем больше его сопротивление электрическому току. Весомое значение имеет также материал, из которого изготовлен проводник.
Как измерять электрического сопротивление?
Для измерения электрического сопротивления необходимо придерживаться следующих правил:
- Измерение проводить нужно параллельно элементу электрического цепи;
- Элемент должен быть обесточен;
- Элемент не должен быть подключен к электрической цепи;
- Измерение имеет смысл только для обычного резистора.
Значение омического сопротивления лучше всего определять с помощью цифрового мультиметра, чтобы избежать ошибок и неточностей в показаниях.
При измерении с помощью измерительного прибора измеряемый элемент не должен быть подключен к источнику напряжения во время измерения. Измеряемый элемент должен быть отпаян от электрической цепи, по крайней мере, с одной стороны. В противном случае расположенные параллельно элементы будут влиять на результат измерения.
|
Перетаскивание зависит от Один из способов справиться со сложными зависимостями — охарактеризовать
Для данного воздуха
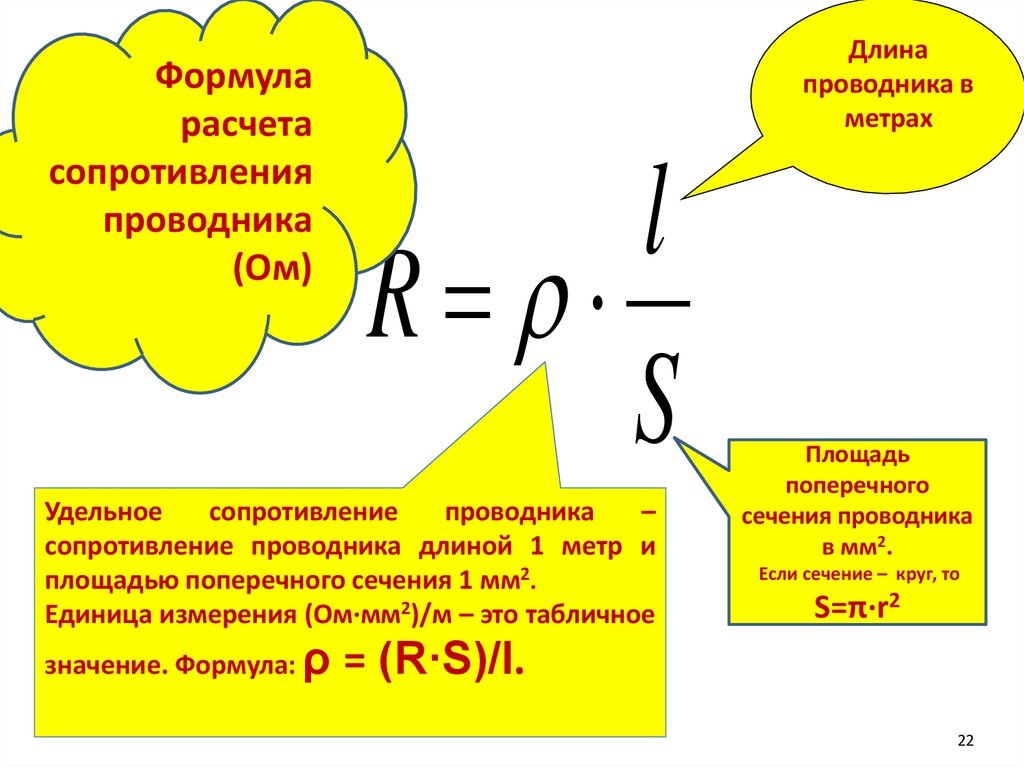
Обратите внимание, что площадь (A), заданная в уравнении сопротивления, представлена как
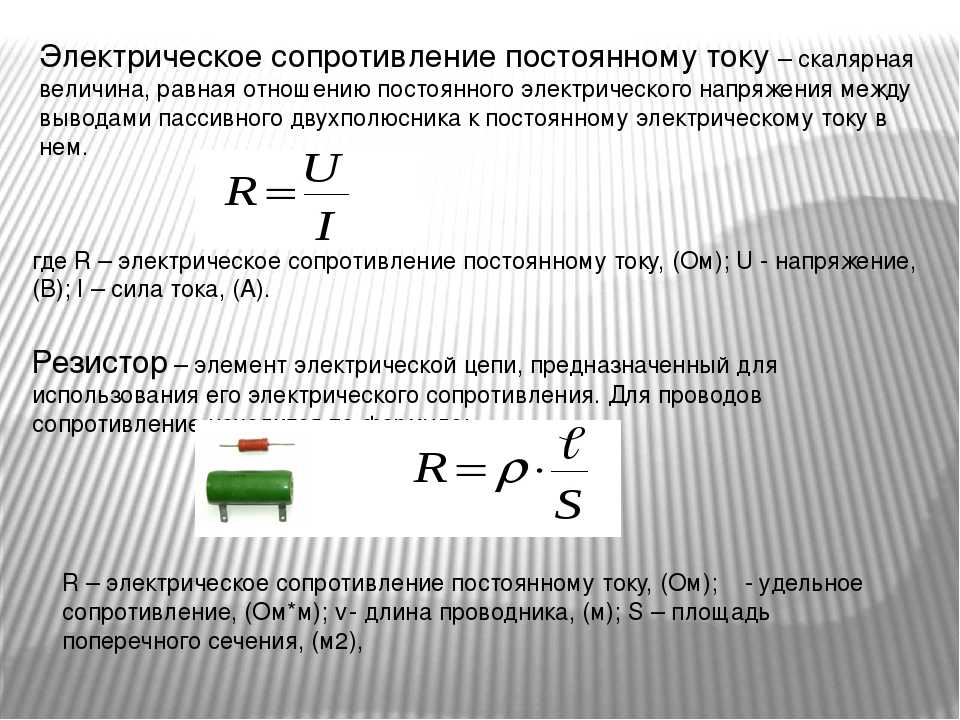
В приведенном выше уравнении плотность обозначается как Экскурсии с гидом
Деятельность: Связанные сайты: |
Силы сопротивления | Физика
Цели обучения
К концу этого раздела вы сможете:
- Выразите математически силу сопротивления.
- Обсудите применение силы сопротивления.
- Задайте конечную скорость.
- Определить конечную скорость при заданной массе.
Другой интересной силой в повседневной жизни является сила сопротивления объекта, когда он движется в жидкости (газе или жидкости).

, где C — коэффициент сопротивления, A — площадь объекта, обращенного к жидкости, а ρ — плотность жидкости.
Спортсмены, а также конструкторы автомобилей стремятся уменьшить силу сопротивления, чтобы сократить время своих гонок. (См. рис. 1). «Аэродинамическая» форма автомобиля может уменьшить силу сопротивления и, таким образом, увеличить расход топлива автомобиля.
Рис. 1. От гоночных автомобилей до бобслеистов аэродинамическая форма имеет решающее значение для достижения максимальной скорости. Бобслей создан для скорости. Они имеют форму пули с коническими плавниками. (кредит: армия США, Wikimedia Commons)
Значение коэффициента аэродинамического сопротивления, C , определяется опытным путем, обычно с использованием аэродинамической трубы. (См. рис. 2).
Рис. 2. Исследователи НАСА тестируют модель самолета в аэродинамической трубе. (кредит: НАСА/Эймс)
Коэффициент лобового сопротивления может зависеть от скорости, но мы будем считать, что здесь он является константой. В таблице 1 перечислены некоторые типичные коэффициенты сопротивления для различных объектов. Обратите внимание, что коэффициент сопротивления является безразмерной величиной. На скоростях шоссе более 50% мощности автомобиля используется для преодоления сопротивления воздуха. Наиболее экономичная крейсерская скорость составляет около 70–80 км / ч (около 45–50 миль / ч).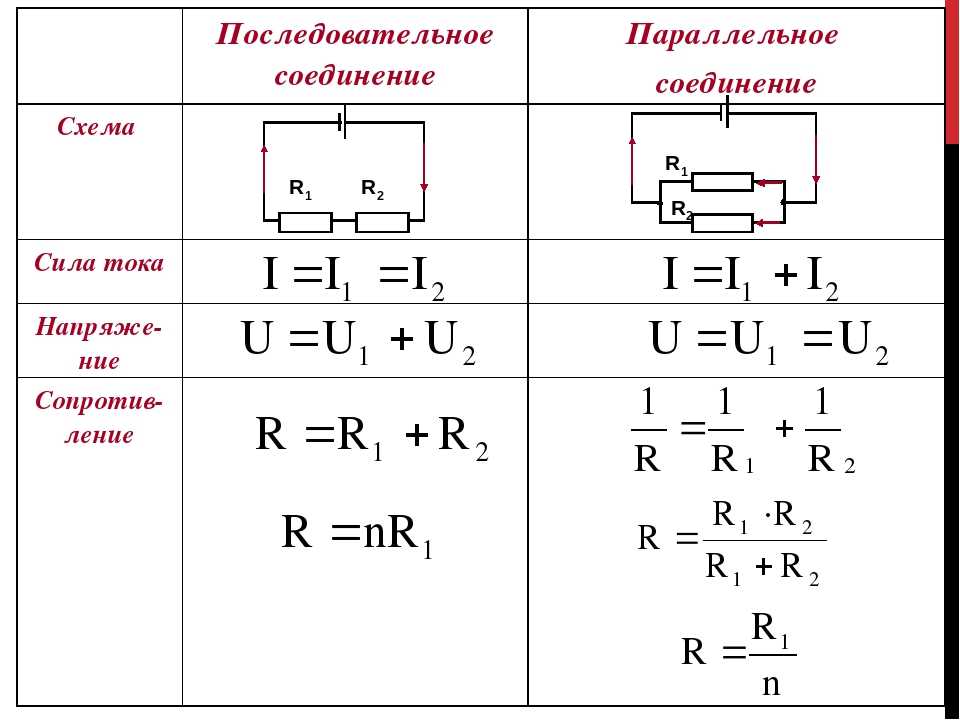
| Таблица 1. Значения коэффициента лобового сопротивления Типичные значения коэффициента лобового сопротивления C . | |
|---|---|
| ОБЪЕКТ | С |
| Аэродинамический профиль | 0,05 |
| Тойота Камри | 0,28 |
| Форд Фокус | 0,32 |
| Хонда Сивик | 0,36 |
| Феррари Тестаросса | 0,37 |
| Пикап Dodge Ram | 0,43 |
| Сфера | 0,45 |
| Внедорожник Hummer h3 | 0,64 |
| Парашютист (ногами вперед) | 0,70 |
| Велосипед | 0,90 |
| Парашютист (горизонтальный) | 1,0 |
| Круглая плоская пластина | 1. 12 12 |
Рисунок 3. Боди, такие как этот LZR Racer Suit, установили множество мировых рекордов после их выпуска в 2008 году. Более гладкая «кожа» и большее усилие сжатия на теле пловца обеспечивают как минимум на 10 % меньше сопротивления. (Фото: НАСА/Кэти Барнсторф)
В мире спорта ведутся серьезные исследования по минимизации сопротивления. Ямочки на мячах для гольфа переделываются, как и одежда, которую носят спортсмены. Велогонщики, а также некоторые пловцы и бегуны носят полные боди. Австралийка Кэти Фриман носила полный костюм на Олимпийских играх 2000 года в Сиднее и выиграла золотую медаль в беге на 400 метров. Многие пловцы на Олимпийских играх 2008 года в Пекине носили комбинезоны (спидометры); это могло бы иметь значение для побития многих мировых рекордов (см. рис. 3). Большинство элитных пловцов (и велосипедистов) бреют волосы на теле. Такие инновации могут сократить миллисекунды в гонке, иногда определяя разницу между золотой и серебряной медалью.
Некоторые интересные ситуации, связанные со вторым законом Ньютона, возникают при рассмотрении воздействия сил сопротивления на движущийся объект. Например, рассмотрим парашютиста, падающего в воздухе под действием силы тяжести. На него действуют две силы: сила тяжести и сила сопротивления (без учета выталкивающей силы). Нисходящая сила тяжести остается постоянной независимо от скорости, с которой движется человек. Однако по мере увеличения скорости человека величина силы сопротивления увеличивается до тех пор, пока величина силы сопротивления не сравняется с силой гравитации, что приводит к нулевой чистой силе. Нулевая результирующая сила означает, что ускорение отсутствует, как указано во втором законе Ньютона. В этот момент скорость человека остается постоянной, и мы говорим, что человек достиг своего 9{2}\right)}}\\ & =& \text{98 м/с}\\ & =& \text{350 км/ч}\text{.
Это означает, что парашютист массой 75 кг достигает максимальной конечной скорости около 350 км/ч, путешествуя в положении согнувшись (головой вперед), сводя к минимуму площадь и сопротивление. В расправленном положении эта конечная скорость может уменьшиться примерно до 200 км/ч по мере увеличения площади. Эта конечная скорость становится намного меньше после раскрытия парашюта.
Возьми домой эксперимент
В этом интересном занятии исследуется влияние веса на конечную скорость. Соберите вместе несколько вложенных фильтров для кофе. Оставив их в исходной форме, измерьте время, за которое один, два, три, четыре и пять вложенных фильтров упадут на пол с одинаковой высоты (примерно 2 м). (Обратите внимание, что из-за того, что фильтры вложены друг в друга, сопротивление постоянно, а изменяется только масса.) Они довольно быстро достигают конечной скорости, поэтому найдите эту скорость как функцию массы. Постройте конечную скорость v по сравнению с массой.
Таким образом, конечная скорость v t может быть записана как [латекс]v_{\text{t}}\sqrt{\frac{2mg}{\rho{CA}}}\\[/latex].
Решение
Все величины известны, кроме площади проекции человека. Это взрослый (82 кг) падающий распростертый орел. Мы можем оценить фронтальную площадь как A = (2 м)(0,35 м) = 0,70 м 2 .
Используя наше уравнение для v , мы находим, что
[латекс]\begin{array}{lll}{v}_{\text{t}}& =& \sqrt{\frac{2\left( \текст{85}\текст{кг}\справа)\слева(9{2}\right)}}\\ & =& \text{44 м/с.}\end{array}\\[/latex]
Обсуждение
Этот результат согласуется со значением для v т упомянутый ранее. 75-килограммовый парашютист, идущий вперед ногами, имел v = 98 м/с. Он весил меньше, но имел меньшую лобовую площадь и, следовательно, меньшее сопротивление воздуха.
Размер объекта, падающего в воздухе, представляет собой еще одно интересное применение сопротивления воздуха.
Следующая интересная цитата о размерах животных и конечной скорости взята из эссе 1928 года британского биолога Дж.Б.С. Холдейна под названием «О том, чтобы быть подходящего размера».
Для мышей и любых мелких животных [гравитация] практически не представляет опасности. Вы можете бросить мышь в шахту длиной в тысячу ярдов; и, достигнув дна, он получает легкий толчок и уходит, при условии, что земля достаточно мягкая. Крыса убита, человек разбит, а лошадь забрызгана. Ибо сопротивление воздуха движению пропорционально поверхности движущегося объекта. Разделите длину, ширину и высоту животного на десять; его вес уменьшен в тысячную, а поверхность только в сотые. Таким образом, сопротивление падению маленького животного относительно в десять раз превышает движущую силу.

Приведенная выше квадратичная зависимость сопротивления воздуха от скорости не выполняется, если объект очень мал, движется очень медленно или находится в более плотной среде, чем воздух. Тогда мы находим, что сила сопротивления прямо пропорциональна скорости. Это соотношение задается законом Стокса , который гласит, что F с = 6 πrηv , где r — радиус объекта, η — вязкость жидкости, а — вязкость жидкости. — скорость объекта.
Закон Стоукса
F S = 6 πrηv , где R является радиусом объекта, η является вязкостью жидкости, а V — это Velocity.
Рис. 4. Гуси летят V-образным строем во время длительных миграционных перемещений. Эта форма снижает сопротивление и потребление энергии для отдельных птиц, а также позволяет им лучше общаться. (кредит: Julo, Wikimedia Commons)
Хорошими примерами этого закона являются микроорганизмы, пыльца и частицы пыли.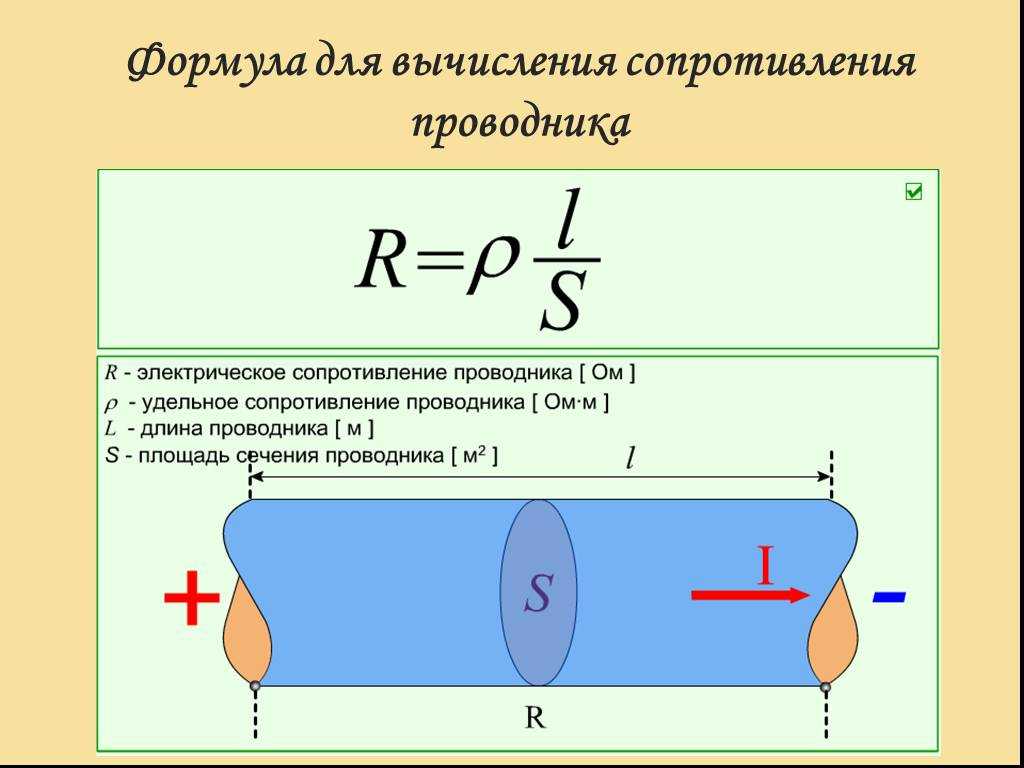
Если мы сравним животных, живущих на суше, с животными, живущими в воде, то увидим, как сопротивление повлияло на эволюцию. Рыбы, дельфины и даже массивные киты имеют обтекаемую форму, чтобы уменьшить силы сопротивления. Птицы имеют обтекаемую форму, а мигрирующие виды, которые летают на большие расстояния, часто имеют особые черты, такие как длинная шея. Стаи птиц летят в форме наконечника копья, формируя обтекаемый рисунок (см.
Эксперимент Галилея
Говорят, что Галилей сбросил с Пизанской башни два объекта разной массы. Он измерил, сколько времени потребовалось каждому, чтобы достичь земли. Поскольку секундомеры были недоступны, как, по-вашему, он измерял время их падения? Если бы объекты были одного размера, но разной массы, что, по вашему мнению, он должен был бы наблюдать? Был бы этот результат другим, если бы это было сделано на Луне?
PhET Исследования: массы и пружины
Реалистичная лаборатория масс и пружин. Подвесьте грузы к пружинам и отрегулируйте жесткость пружины и демпфирование. Вы даже можете замедлить время. Перевозите лабораторию на разные планеты. Диаграмма показывает кинетическую, потенциальную и тепловую энергию для каждой пружины. 9{2}\\[/latex], где C – коэффициент сопротивления (типичные значения приведены в таблице 1), A – площадь объекта, обращенная к жидкости, а [латекс]\rho\\[ /латекс] — плотность жидкости.
Концептуальные вопросы
- Спортсмены, такие как пловцы и велосипедисты, на соревнованиях носят комбинезоны. Сформулируйте список плюсов и минусов таких костюмов.
- Для силы сопротивления, испытываемой движущимся объектом в жидкости, использовались два выражения. Один зависел от скорости, а другой был пропорционален квадрату скорости. К каким видам движения каждое из этих выражений будет более применимо, чем другое?
- Во время движения автомобилей масло и бензин вытекают на дорожное покрытие. Если идет легкий дождь, как это влияет на управляемость автомобиля? Имеет ли значение сильный дождь?
- Почему белка может спрыгнуть с ветки дерева на землю и убежать невредимой, а человек при таком падении может сломать кость?
Задачи и упражнения
- Конечная скорость человека, падающего в воздухе, зависит от веса и площади тела человека, обращенного к жидкости.
Найти конечную скорость (в метрах в секунду и километрах в час) парашютиста массой 80,0 кг, падающего в положении «согнувшись» (головой вперед) с площадью поверхности 0,140 м 2 .
- Парашютист весом 60 кг и 90 кг прыгают с самолета на высоте 6000 м, оба падают в положении «согнувшись». Сделайте некоторое предположение об их лобовых площадях и рассчитайте их конечные скорости. Сколько времени потребуется каждому парашютисту, чтобы достичь земли (при условии, что время достижения конечной скорости мало)? Предположим, что все значения имеют точность до трех значащих цифр.
- Белка массой 560 г и площадью поверхности 930 см 2 падает с дерева высотой 5,0 м на землю. Оцените его конечную скорость. (Используйте коэффициент аэродинамического сопротивления для горизонтального парашютиста.) Какова будет скорость человека массой 56 кг, который упадет на землю, при условии отсутствия сопротивления на таком коротком расстоянии?
- Чтобы поддерживать постоянную скорость, сила, создаваемая двигателем автомобиля, должна равняться силе сопротивления плюс сила трения о дорогу (сопротивление качению).
(a) Каковы величины сил сопротивления при скорости 70 км/ч и 100 км/ч для Toyota Camry? (площадь сопротивления равна 0,70 м 2 ) (b) Какова величина силы сопротивления при скорости 70 км/ч и 100 км/ч для Hummer h3? (Площадь сопротивления составляет 2,44 м 2 ) Предположим, что все значения точны до трех значащих цифр.
- Во сколько раз увеличивается сила сопротивления автомобиля при движении от 65 до 110 км/ч?
- Рассчитайте скорость, с которой сферическая капля дождя падает с высоты 5,00 км (a) в отсутствие сопротивления воздуха (b) с сопротивлением воздуха. Примем размер капли поперек 4 мм, плотность 1,00 × 10 3 кг/м 3 и площадь поверхности π r 2 .
- Используя закон Стокса, убедитесь, что единицами измерения вязкости являются килограммы на метр в секунду.
- Найдите конечную скорость шарообразной бактерии (диаметром 2,00 мкм), падающей в воду. Сначала вам нужно отметить, что сила сопротивления равна весу при конечной скорости.
Примем плотность бактерии равной 1,10 × 10 3 кг/м 3 .
- Закон Стокса описывает осаждение частиц в жидкостях и может использоваться для измерения вязкости. Частицы в жидкостях быстро достигают предельной скорости. Можно измерить время, за которое частица падает на определенное расстояние, а затем использовать закон Стокса для расчета вязкости жидкости. Предположим, что стальной шарикоподшипник (плотность 7,8 × 10 3 кг/м 3 , диаметр 3,0 мм) брошен в емкость с моторным маслом. Падение с высоты 0,60 м занимает 12 с. Рассчитайте вязкость масла. 9{2}\\[/latex], где C – коэффициент сопротивления, A – площадь объекта, обращенного к жидкости, а [latex]\rho[/latex] – плотность жидкости
Закон Стокса: [латекс]{F}_{s}=6\pi{r}\eta{v}\\[/latex] , где r — радиус объекта, η — вязкость жидкости, а v – скорость объекта
Избранные решения задач и упражнений
1.


 Определение стоимости
Определение стоимости И
И Мы не используем «d» для плотности
Мы не используем «d» для плотности
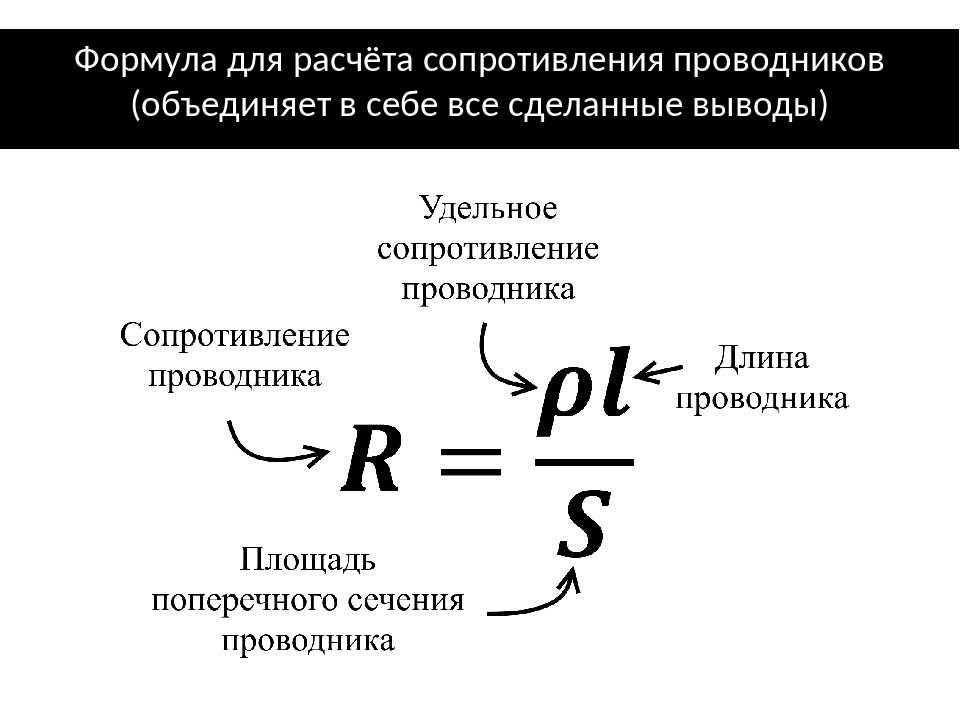 Найти конечную скорость (в метрах в секунду и километрах в час) парашютиста массой 80,0 кг, падающего в положении «согнувшись» (головой вперед) с площадью поверхности 0,140 м 2 .
Найти конечную скорость (в метрах в секунду и километрах в час) парашютиста массой 80,0 кг, падающего в положении «согнувшись» (головой вперед) с площадью поверхности 0,140 м 2 .  (a) Каковы величины сил сопротивления при скорости 70 км/ч и 100 км/ч для Toyota Camry? (площадь сопротивления равна 0,70 м 2 ) (b) Какова величина силы сопротивления при скорости 70 км/ч и 100 км/ч для Hummer h3? (Площадь сопротивления составляет 2,44 м 2 ) Предположим, что все значения точны до трех значащих цифр.
(a) Каковы величины сил сопротивления при скорости 70 км/ч и 100 км/ч для Toyota Camry? (площадь сопротивления равна 0,70 м 2 ) (b) Какова величина силы сопротивления при скорости 70 км/ч и 100 км/ч для Hummer h3? (Площадь сопротивления составляет 2,44 м 2 ) Предположим, что все значения точны до трех значащих цифр.  Примем плотность бактерии равной 1,10 × 10 3 кг/м 3 .
Примем плотность бактерии равной 1,10 × 10 3 кг/м 3 . 
Добавить комментарий