Что такое разность фаз: Разность фаз напряжения и тока

Содержание

Разность фаз напряжения и тока

[email protected]

Узнать больше Помощь в заказе

Условимся под разностью фаз φ напряжения и тока всегда понимать разность начальных фаз напряжения и тока (а не наоборот):

Поэтому на векторной диаграмме угол φ отсчитывается в направлении от вектора I к вектору U (рис. 3.10). Именно при таком определении разности фаз угол φ равен аргументу комплексного сопротивления. Угол φ положителен при отстающем токе () и отрицателен при опережающем токе ().
Разность фаз между напряжением и током зависит от соотношения индуктивного и емкостного сопротивлений. При имеем и ток отстает по фазе от напряжения, . При имеем , ток совпадает по фазе с напряжением, rLC-цепь в целом проявляет себя как активное сопротивление. Это случай так называемого резонанса в последовательном контуре. Наконец, при имеем , ток опережает по фазе напряжение.

Векторные диаграммы для трех возможных соотношений даны на рис. 3.11. При построении этих диаграмм начальная фаза тока ; принята равной нулю. Поэтому равны друг другу.
Рассматривая при заданной частоте цепь по рис. 3.8 в целом как пассивный двухполюсник, можно ее представить одной из трех эквивалентных схем: при как последовательное соединение сопротивления и индуктивности (), при как сопротивление r и при как последовательное соединение сопротивления и емкости (). При заданных L и С соотношение между зависит от частоты, а потому от частоты зависит и вид эквивалентной схемы.
Выше, в разделе, было принято, что задан ток, а определялись напряжения на элементах и на входных выводах цепи. Однако часто бывает задано напряжение на выводах, а ищется ток. Решение такой задачи не представляет труда. Записав по заданным величинам комплексное напряжение U и комплексное сопротивление Z, определим комплексный ток

и тем самым действующий ток и начальную фазу тока.
Часто равной нулю принимается начальная фаза заданного напряжения: . В этом случае, как следует из раздела, начальная фаза тока ; равна и противоположна по знаку разности фаз φ, т. е .
Установленные выше соотношения между амплитудами и действующими токами и напряжениями, а также выражение для сдвига фаз ф позволяют вычислить ток и не прибегая к записи закона Ома в комплексной форме. Подробно этот путь решения показан в примере 3.4.

Пример 3.4.
К цепи, состоящей из последовательно соединенных конденсатора и катушки, приложено напряжение . Емкость конденсатора С=5 мкФ, сопротивление катушки r=15 Ом, индуктивность L=12 мГн. Найти мгновенные значения тока в цепи и напряжений на конденсаторе и на катушке.

Решение.
Схема замещения цепи показана на рис. 3.8.

Напряжение на емкости отстает от тока по фазе на 90°, следовательно,

Комплексное сопротивление катушки

Комплексная амплитуда напряжения на выводах катушки

Мгновенное напряжение на катушке

Пример 3.5.
В цепи, состоящей из последовательно соединенных конденсатора и катушки, ток I=2 А, его частота f=50 Гц.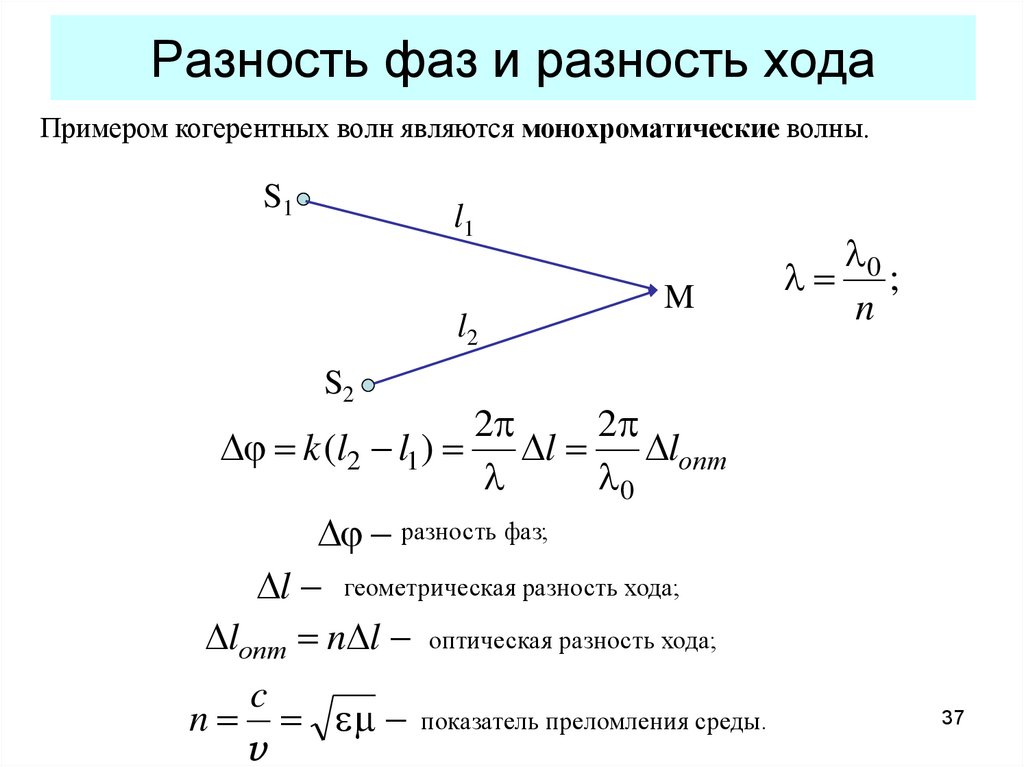 Напряжение на выводах цепи U=100 В, катушки U_кат =150 В и конденсатора U_с=200 В. Определить сопротивление и индуктивность катушки и емкость конденсатора.

Решение.

Полное сопротивление цепи z=U/I=50 Ом.
Полное сопротивление катушки zкат=Uкат/I=75 Ом;

Все страницы раздела «Цепи переменного тока» на websor

Разность фаз тока и напряжения

В общем случае
ток и напряжение достигают своих
максимальных значений не одновременно.
При этом говорят, что имеет место разность
фаз тока и
напряжения (сдвиг
по фазе).

Разностью
фаз тока и
напряжения называется доля периода, на
которую одна функция опережает другую
(или отстает от нее).

При этом если
ток по фазе
отстает от напряжения,
разность фаз считается положительной
(φ >0), в противном случае разность фаз
считается отрицательной
(φ<0). Нередко
разность фаз измеряют не в долях периода,
а в угловых градусах. При этом полный
период соответствует 360⁰_.
В примере, приведенном на рис.2.1, ток
опережает напряжение, значит, φ <0.

φ
= —
^°

Приведенный
пример определяет метод измерения
разности фаз: измерив по шкале на экране
осциллографа
и Т, разность фаз можно определить по
формуле:

φ
=
(2.10)

Производить
операции над синусоидальными величинами,
изменяющимися с одинаковой частотой
(например, складывать или вычитать,
умножать на число, большее нуля), гораздо
проще, если изображать их в виде
векторов.

На векторной
диаграмме синусоидальные функции
условно представляются в виде векторов,
длины
которых в масштабе соответствуют
действующим
значениям
этих функций. Углы
между векторами равны разностям
фаз
соответствующих функций.

Направление
одного из векторов (так называемого
опорного вектора) выбирается произвольно.
При этом порядок следования векторов
(отставание, опережение) определяется
при мысленном вращении диаграммы против
часовой стрелки. Как уже говорилось,
на векторных диаграммах токов и напряжений
положительная разность фаз (φ >0)
означает, что ток отстает от напряжения,
и наоборот.

Пример 1.
Построить векторную диаграмму: U=20
В,I=15
мА,

φ= — 45⁰

Последовательность
действий:

Выбираем масштаб
тока и напряжения (независимо друг от
друга). Указывать масштаб можно разными
способами, например, так:

МU:
0,5;
МI:
0,6
;

или графически:
5 В 3 мА

Выбираем опорный
вектор, определяем его длину в масштабе.
Откладываем разность фаз по часовой
или против часовой стрелки в зависимости
от знака разности фаз φ.
Чертим другой
вектор в соответствующем масштабе и
под углом φ к опорному вектору.

Рис.
2.2

Пример 2. По
некоторому участку цепи протекают токи:
I₁=60
мА,

I₂=40
мА, I₃=90
мА

Разности фаз
токов с напряжением соответственно
равны: φ₁
= 90⁰,

φ₂= 0⁰,

φ₃
= -90⁰.

Чемуравен
результирующий ток?

Решение:

Построим векторную
диаграмму, то есть сложим векторы токов:

_=

++

В
качестве опорного выбираем вектор
,
одинаковый для всех токов. При сложении
векторов каждый следующий вектор
проводится из конца предыдущего.
Результирующим является вектор,
проведенный из начала первого в конец
последнего вектора. (Рис.2.3)

Масштаб:
10 мА

Рис.
2.3

Рядом с
чертежом необходимо указать масштаб.
Величину результирующего тока I
определяют с помощью линейки и указанного
масштаба. В данном случае, так как углы
между векторами составляют 90⁰,
величину тока I
можно найти по теореме Пифагора:
I
=
==
50 (мА)

Результирующий
ток I
опережает напряжение U
на угол φ< 0.

Элементы в цепи
переменного тока.

В электротехнике
наиболее распространены три вида
элементов:

1) резистивный;
2) индуктивный;
3) емкостный.

Разность фаз: определение, формула и уравнение

Фаза волны представляет собой долю цикла волны . В волне полный цикл от гребня до гребня или впадины до впадины равен 2π [рад]. Таким образом, каждая часть этой длины меньше 2π [рад]. Половина цикла равна π [рад], а четверть цикла равна π/2 [рад]. Фаза измеряется в радианах, которые являются безразмерными единицами.

Рис. 1. Волновые циклы делятся на радианы, причем каждый цикл охватывает расстояние в 2π [рад]. Циклы повторяются через 2π [рад] (красные значения). Каждое значение больше 2π [рад] является повторением значений от 0π [рад] до 2π [рад]

Формула фазы волны

Чтобы рассчитать фазу волны в произвольной позиции, вам необходимо определить, насколько далеко эта позиция находится от начала вашего цикла волны. В простейшем случае, если ваша волна может быть аппроксимирована функцией синуса или косинуса, ваше волновое уравнение можно упростить следующим образом:

\[y = A \cdot \sin(x)\]

Здесь A — максимум амплитуда волны, x — значение на горизонтальной оси, которое повторяется от 0 до 2π для функций синуса/косинуса, а y — высота волны в точке x.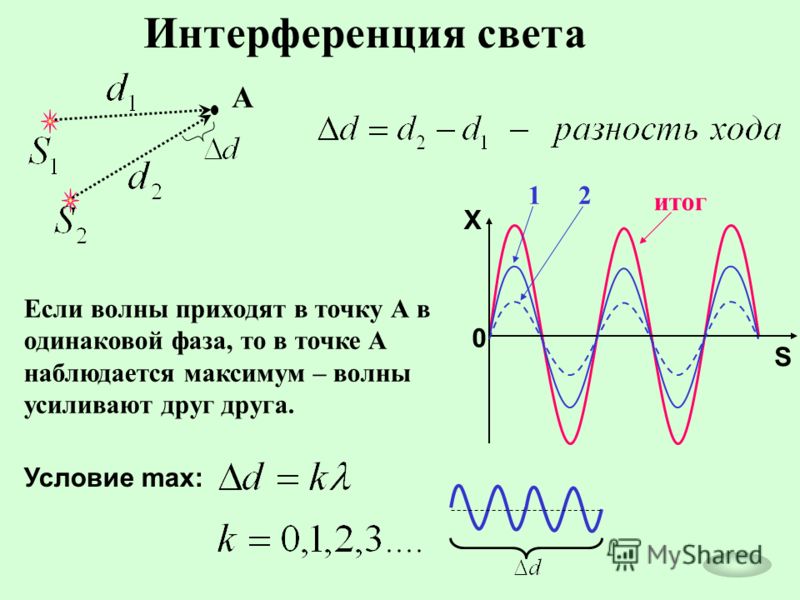 Фаза любой точки x может быть определена с помощью приведенного ниже уравнения: 9{\circ}}{\pi}\]

Иногда волна может быть представлена выражением, таким как \(y = A \cdot \sin(x — \phi)\). В этих случаях волна сдвинута по фазе на \(\phi\) радиан.

Разность фаз волн

Разность фаз волн возникает, когда две волны движутся и их циклы не совпадают. Разность фаз известна как разность циклов между двумя волнами в одной и той же точке.

Перекрывающиеся волны с одинаковым циклом называются волнами в фазе, а волны с разностью фаз, которые не перекрываются, называются несовпадающими по фазе. Волны, которых не в фазе могут компенсировать друг друга из , а волны в фазе могут усиливать друг друга .

Формула разности фаз

Если две волны имеют одинаковую частоту/период, мы можем вычислить их разность фаз. Нам нужно будет вычислить разницу в радианах между двумя гребнями, которые находятся рядом друг с другом, как показано на следующем рисунке.

Рис. 2. Разница фаз между двумя волнами i(t) и u(t), меняющимися во времени (t), вызывает пространственную разницу в их распространении 9\circ} = \frac{\pi}{12}\]

Вычитая обе фазы, получаем разность фаз:

\[\Delta \phi = \phi(15) — \phi(30) = \frac {\pi}{12}\]

В этом случае мы видим, что волны сдвинуты по фазе на π / 12, что составляет 15 градусов.

Волны в фазе

Когда волны в фазе, их гребни и впадины совпадают друг с другом, как показано на рисунке 3. Волны в фазе испытывают конструктивную интерференцию. Если они изменяются во времени (i(t) и u(t)), они объединяют свою интенсивность (справа: фиолетовый).

Рис. 3 – Конструктивная интерференция

Волны в противофазе

Волны в противофазе создают неравномерную картину колебаний, так как гребни и впадины не перекрываются. В крайних случаях, когда фазы сдвинуты на π [рад] или на 180 градусов, волны компенсируют друг друга, если они имеют одинаковую амплитуду (см. рисунок ниже). В этом случае говорят, что волны находятся в противофазе, и эффект этого известен как деструктивная интерференция.

Рис. 4. Противофазные волны испытывают деструктивную интерференцию. В этом случае волны \(i(t)\) и \(u(t)\) имеют разность фаз \(180\) градусов, заставляя их компенсировать друг друга

Разность фаз в различных волновых явлениях

Разность фаз вызывает различные эффекты в зависимости от волновых явлений, которые можно использовать для многих практических приложений.

Сейсмические волны : системы пружин, масс и резонаторов используют циклическое движение для противодействия вибрациям, создаваемым сейсмическими волнами. Системы, установленные во многих зданиях, уменьшают амплитуду колебаний, тем самым снижая структурные напряжения.
Технологии шумоподавления : Многие технологии шумоподавления используют систему датчиков для измерения входящих частот и создания звукового сигнала, который подавляет эти входящие звуковые волны. Таким образом, входящие звуковые волны уменьшают свою амплитуду, что в звуке напрямую связано с интенсивностью шума.
Энергетические системы: где используется переменный ток, напряжение и ток могут иметь разность фаз. Это используется для идентификации цепи, поскольку его значение будет отрицательным в емкостных цепях и положительным в индуктивных цепях.

Сейсмическая технология опирается на системы пружинных масс для противодействия движению сейсмических волн, как, например, в башне Taipei 101. Маятник представляет собой шар весом 660 метрических тонн. Когда сильный ветер или сейсмические волны обрушиваются на здание, маятник качается взад и вперед, качаясь в направлении, противоположном направлению движения здания.

Рис. 5 — Движение маятника на башне Taipei 101 не совпадает по фазе с движением здания на 180 градусов. Силам, действующим на здание (Fb), противодействует сила маятника (Fp) (маятник – сфера).

Маятник уменьшает колебания здания, а также рассеивает энергию, действуя как демпфер настроенной массы.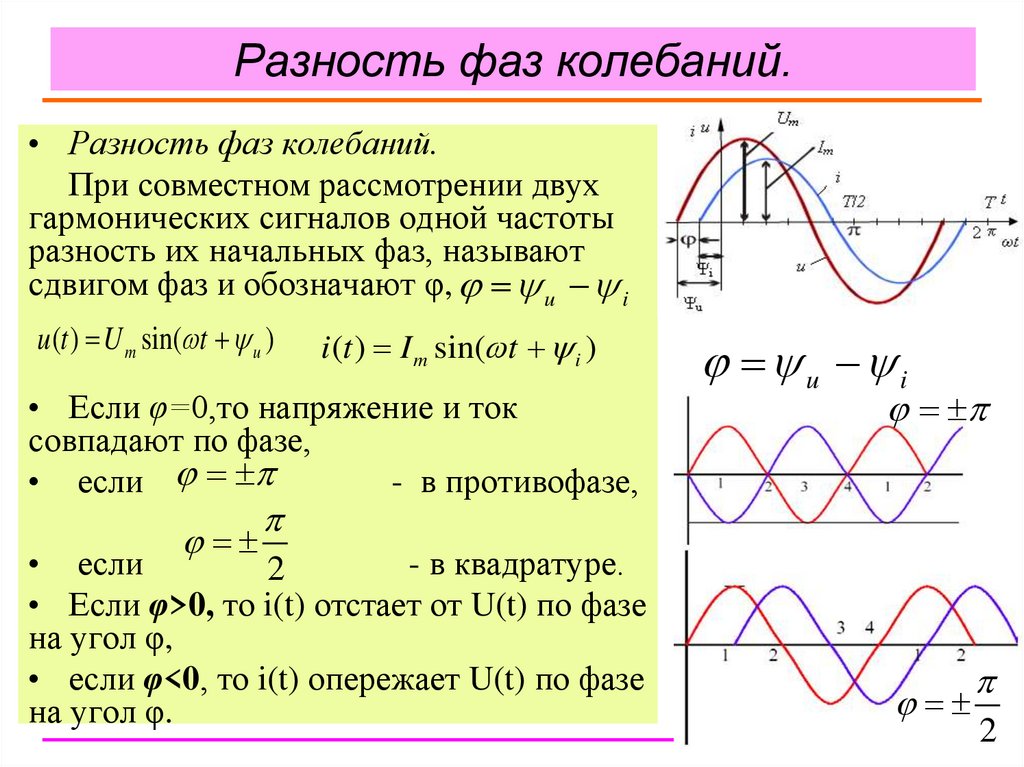 Пример маятника в действии наблюдался в 2015 году, когда из-за тайфуна шарик маятника качнулся более чем на метр.

Разность фаз – основные выводы

Разность фаз – это значение, представляющее часть цикла волны.
В фазе волны перекрываются и создают конструктивную интерференцию, увеличивающую их максимумы и минимумы.
Несовпадающие по фазе волны создают деструктивную интерференцию, которая создает нерегулярные узоры. В крайних случаях, когда волны сдвинуты по фазе на 180 градусов, но имеют одинаковую амплитуду, они компенсируют друг друга.
Разность фаз была полезна для создания технологий смягчения сейсмических воздействий и шумоподавления.

Разность фаз и фазовый сдвиг

Положение волновой частицы периодической формы волны известно как «Фаза» волны. Полная фаза полного цикла сигнала составляет 360 ⁰ .

Когда две или более волны одной частоты интерферируют в среде или движутся по одному и тому же пути, «фаза» волн играет важную роль для получения желаемого результата без возникновения шума.

Фазу также можно определить как «Относительное смещение двух волн относительно друг друга».

Фаза также может быть выражена в радианах и градусах. Один радиан = 57,3 градуса.

Схема

Разность фаз

Разность фаз синусоидальной волны можно определить как «интервал времени, на который волна опережает или отстает от другой волны», и разность фаз не является свойством только одной волны, это относительное свойство до двух и более волн. Это также называется «фазовым углом» или «фазовым смещением».

Разность фаз, представленная греческой буквой фи (Φ). Полная фаза сигнала может быть определена как 2π радиан или 360 градусов.

Опережающая фаза означает, что сигнал опережает другой сигнал с той же частотой, а Отстающая фаза означает, что сигнал отстает от другого сигнала с той же частотой.

Фазовая квадратура: Когда разность фаз между двумя волнами составляет 90 ⁰ (это может быть = + 90 ⁰ или – 90 ⁰ ), говорят, что волны находятся в «фазовой квадратуре».

Противофаза: когда разность фаз между двумя волнами составляет 180 ⁰ (это может быть = + 180 ⁰ или — 180 ⁰ ), тогда говорят, что волны находятся в «фазовой оппозиции».

Чтобы лучше понять эту концепцию, обратите внимание на рисунок ниже.

Временной интервал и фаза сигнала обратно пропорциональны друг другу. Это означает, что

t град = 1 / (360 f ) (градусы)

t рад = 1 / (6,28 f ) (радиан)

Где f — частота сигнала, а t — период времени.

Например, если две синусоидальные волны имеют одинаковую частоту и фазовый сдвиг π/2 радиан, то фазы волн можно определить как (nπ + 1) и nπ радиан.

Фазовый сдвиг сигналов также может быть представлен в виде периода времени (T). Например, +6 мс и – 7 мс и т. д.

Вернуться к началу

Уравнение разности фаз

Разность фаз синусоидальных сигналов может быть выражена приведенным ниже уравнением, используя максимальное напряжение или амплитуду сигналов,

A _(t) = A _max × sin(ωt±Ø)

Где

Amax – амплитуда синусоиды измерений

ωt – угловая скорость (радиан/с)

Φ – фазовый угол. (Радианы или градусы)

Если Φ < 0, то говорят, что фазовый угол волны находится в отрицательной фазе. Точно так же, если Φ > 0, то говорят, что фазовый угол волны находится в положительной фазе.

Соотношение фаз синусоидальной волны

Каждая переменная форма волны будет иметь свой ток, напряжение и частоту. Если напряжение и угловые скорости двух сигналов одинаковы, то их фаза также одинакова в любой момент времени.

На приведенном выше рисунке мы видим три волны, которые начинаются в начале координат, ведут в начале координат и отстают в начале координат соответственно.

Наверх

Разность фаз сигналов

Вне фазы

Когда чередующиеся сигналы имеют одинаковую частоту, но разные фазы, говорят, что они «вне фазы». Разность фаз не равна нулю для расфазированных волн. Обратите внимание на приведенный ниже рисунок, который описывает несовпадающую по фазе концепцию двух синусоидальных волн. Для синфазных сигналов запаздывание составляет доли длины волны, такие как 1/2, 2/3, 3/5… и т. д.

0 ⁰ (Φ = 90 ⁰ ) к волне «А». Таким образом, мы можем сказать, что две волны не совпадают по фазе.

Для волн, не совпадающих по фазе, есть два условия. Это

1. Опережающая фаза

2. Отстающая фаза

Опережающая фаза

Когда два сигнала одной и той же частоты движутся вдоль одной и той же оси, и один сигнал опережает другой, тогда это называется опережающим фазовым сигналом. .

Уравнения тока и напряжения для опережающих фазированных сигналов:

Напряжение (Vt) = Vm sin ωt

Ток (it) = Im sin (ωt – Φ)

Где Φ – опережающий фазовый угол.

Отставание по фазе

Когда два сигнала одной частоты движутся вдоль одной и той же оси, и один сигнал отстает от другого, это называется «Отставание по фазе».

Уравнения напряжения и тока для опережающих фазированных сигналов:

Напряжение (Vt) = Vm sin ωt

Ток (it) = Im sin (ωt + Φ)

Где Φ — фазовый угол отставания.

IN Phase Синусоидальные волны

Когда разница между фазами двух чередующихся волн равна нулю, волны называются синфазными. Это может произойти, когда два сигнала имеют одинаковую частоту и одинаковую фазу. Для синфазных сигналов запаздывание представляет собой целое число длин волн, например 0, 1, 2, 3… Синфазные сигналы показаны на рисунке ниже.

Сигналы на изображении выше имеют разную амплитуду (максимальное напряжение), но имеют одинаковую частоту.

Пример: Если две синусоидальные волны A и B не совпадают по фазе, а разность фаз составляет 25 ⁰, то мы можем объяснить соотношение между волнами как

Волна «A» опережает волну «B» на 25 ⁰ или волна ‘B’ отстает от волны ‘A’ на 25 ⁰ . Таким образом, ток и напряжение этих сигналов также изменяются в зависимости от фазового сдвига нефазированных сигналов.