Сигма электростатика: Электростатика | Формулы по физике

Электростатика | Формулы по физике

Электрический заряд

Найти

  Известно, что:

     qne =
  

Вычислить ‘q’

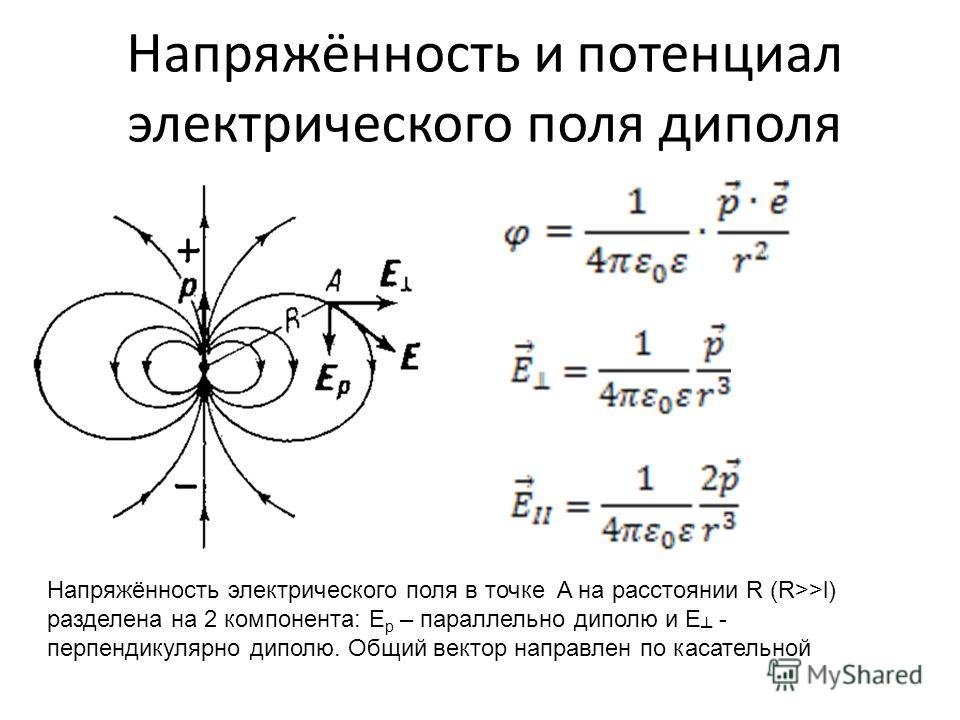
Закон Кулона

Найти

  Известно, что:

     Fkq1q2r =
  

Вычислить ‘F’

Постоянная Кулона

Найти

  Известно, что:

     kπε_0 =
  

Вычислить ‘k’

Относительная диэлектрическая проницаемость

Найти

  Известно, что:

     εF_вакF_окр =
  

Вычислить ‘ε’

Электрическое поле

Найти

  Известно, что:

     EFq =
  

Вычислить ‘E’

Электрическое поле точечного заряда в вакууме

Найти

  Известно, что:

     Ekq_0r =
  

Вычислить ‘E’

Электрическое поле точечного заряда в окружающей среде

Найти

  Известно, что:

     E_окрkq_0εr =
  

Вычислить ‘E_окр’

Электрическое поле вне заряженной сферы

Найти

  Известно, что:

     Ekσ4πRr =
  

Вычислить ‘E’

Электрическое поле вне заряженной сферы

Найти

  Известно, что:

     Ekqr =
  

Вычислить ‘E’

Электрическое поле бесконечной заряженной плоскости

Найти

  Известно, что:

     Ek2πσ =
  

Вычислить ‘E’

Электрическое поле бесконечной заряженной плоскости

Найти

  Известно, что:

     Eσε_0 =
  

Вычислить ‘E’

Электрическое поле конденсатора

Найти

  Известно, что:

     Ekπσ =
  

Вычислить ‘E’

Работа в электрическом поле

Найти

  Известно, что:

     AFΔ_d =
  

Вычислить ‘A’

Потенциальная энергия системы двух точечных зарядов

Найти

  Известно, что:

     Wkq0qεr =
  

Вычислить ‘W’

Работа в электрическом поле — разность потенциальных энергий

Найти

  Известно, что:

     AW1W2 =
  

Вычислить ‘A’

Потенциал электростатического поля

Найти

  Известно, что:

     φWq =
  

Вычислить ‘φ’

Напряжение — разность потенциалов

Найти

  Известно, что:

     Uφ1φ2 =
  

Вычислить ‘U’

Работа переноса заряда

Найти

  Известно, что:

     AqU =
  

Вычислить ‘A’

Потенциал электростатического поля вокруг точечного заряда

Найти

  Известно, что:

     φkq0εr =
  

Вычислить ‘φ’

Напряжённость электростатического поля

Найти

  Известно, что:

     EUΔ_d =
  

Вычислить ‘E’

Результирующее электрическое поле

Найти

  Известно, что:

     EE0E1 =
  

Вычислить ‘E’

Электрический момент

Найти

  Известно, что:

     pql =
  

Вычислить ‘p’

Электрическая ёмкость

Найти

  Известно, что:

     Cqφ =
  

Вычислить ‘C’

Электрическая ёмкость шара

Найти

  Известно, что:

     CεRk =
  

Вычислить ‘C’

Электрическая ёмкость двух проводников

Найти

  Известно, что:

     CqU =
  

Вычислить ‘C’

Электрическая ёмкость плоского конденсатора

Найти

  Известно, что:

     Cεε0Sd =
  

Вычислить ‘C’

Электрическая ёмкость сферического конденсатора

Найти

  Известно, что:

     Cπεε0R1R2 =
  

Вычислить ‘C’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     WqE1d =
  

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     WqEd =
  

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     WqU =
  

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     WCU =
  

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     WqC =
  

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     Wεε0EV =
  

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     Wεε0ESd =
  

Вычислить ‘W’

Плотность энергии электрического поля

Найти

  Известно, что:

     ω_pWV =
  

Вычислить ‘ω_p’

Плотность энергии электрического поля

Найти

  Известно, что:

     ω_pε0εE =
  

Вычислить ‘ω_p’

Что такое «сигма»? • Физика элементарных частиц • LHC на «Элементах»

Сигмой (σ) в статистическом анализе обозначают стандартное отклонение. Опуская тонкости, которые будут обсуждены ниже, можно сказать, что стандартное отклонение — это та погрешность, то «± сколько-то», которым обязательно сопровождают измерение величины. Если вы измерили массу предмета и получили результат 100 ± 5 грамм, то величина «110 грамм» отличается от измеренного результата на два стандартных отклонения (то есть на 2 сигмы), величина «50 грамм» отличается на 10 стандартных отклонений (на 10 сигм).

Зачем всё это нужно: сигмы и вероятности

При обсуждении погрешностей мы уже говорили, что фраза «измеренная масса равна 100 ± 5 грамм» вовсе не означает, что истинная масса гарантированно лежит в интервале от 95 до 105 грамм. Она может оказаться и за пределами этого интервала «± 1σ», но, как правило, недалеко. В небольшом проценте случаев может даже случиться, что она выходит за пределы интервала «± 2σ», и уж совсем редко она оказывается за пределами «± 3σ». В общем, тенденция ясна: количество сигм связано с вероятностью того, что истинное значение будет настолько отличаться от измеренного.

Пропустим все математические подробности и покажем результат для самого простого и распространенного случая, который называется «нормальное распределение» (см. рисунок). Вероятность попасть в интервал ± 1σ — примерно 68%, в интервал ± 2σ — примерно 95%, в интервал ± 3σ — примерно 99,8%, и т. д. Итак, можно сформулировать некую договоренность:

Договоренность: выражение какого-то отличия в количестве сигм — это сообщение о том, какова вероятность, что такое или еще более сильное отличие могло произойти за счет случайного стечения обстоятельств при измерении.

Использовать эту договоренность можно разными способами. Если вы просто сообщаете результат измерения (100 ± 5 грамм) и уверены в том, что нормальное распределение применимо, то вы можете сказать, что истинное значение массы с вероятностью 68% лежит в этом интервале, с вероятностью 95% лежит в интервале от 90 до 110 грамм, и т. д.

Вы можете также сравнивать результат вашего измерения с чужим измерением той же самой величины или с теоретическими расчетами. Вы видите, что числа отличаются, и хотите понять, имеете ли вы право утверждать, что между двумя результатами есть статистически значимое расхождение — то есть несогласие, которое нельзя списать на случайную статистическую флуктуацию в данных. Тогда утверждения звучат так:

• Если отличие составляет меньше 1σ, то вероятность того, что два числа согласуются друг с другом, больше 32%. В таком случае просто говорят, что два результата совпадают в пределах погрешностей.
• Если отличие составляет меньше 3σ, то вероятность того, что два числа согласуются друг с другом, больше 0,2%. В физике элементарных частиц такой вероятности недостаточно для каких-либо серьезных выводов, и принято говорить: различие между двумя результатами не является статистически значимым.
• Если отличие от 3σ до 5σ, то это повод подозревать что-то серьезное. Впрочем, даже в этом случае физики говорят осторожно: данные указывают на существование различия между двумя результатами.
• И только если два результата отличаются на 5σ или больше, физики четко заявляют: два результата отличаются друг от друга.

Эти выражения особенно стандартны, когда речь идет о поиске новой частицы. Вы сравниваете экспериментальные данные с теоретическим предсказанием, сделанным без новой частицы, и, если видите отличие от 3 до 5 сигм, вы говорите: получено указание на существование новой частицы (по-английски, evidence). Если же отличие превышает 5 сигм, вы говорите: мы открыли новую частицу (discovery).

«Уверенность» против «статистической значимости»

Заметьте, что в приведенных выше примерах нас интересовали вопросы, на которые можно ответить «да» или «нет». Проступает ли в полученных данных какая-то новая частица? Согласуется ли распределение по импульсу с теоретическими расчетами? Зависит ли сечение процесса от энергии столкновений? Совпадает ли масса у частицы и ее античастицы? Попытка ответить на эти вопросы с помощью данных называется на научном языке проверкой гипотез. Вопросы, которые требуют развернутого ответа (подсчитать что-то, объяснить что-то и т. п.), гипотезами не называются.

В простейшем приближении результат экспериментальной проверки гипотезы выглядит так: ответ «да» с вероятностью p и ответ «нет» с вероятностью 1 – p. Эти вероятности очень важны для сообщения результата; физики обычно избегают абсолютных утверждений («мы открыли» или «мы опровергли») без указания вероятностей.

Но тут сразу же надо сделать важное уточнение. Если его четко осознать, то станет понятным, почему такие стандартные для научно-популярных новостей фразы, как «Ученые на 99% уверены, что открыли что-то новое», — обманчивы.

Точная формулировка, которую обычно используют ученые, такова:

При проверке гипотезы получен ответ «да» на уровне статистической значимости p.

При этом величина p часто выражается в виде количества сигм. В англоязычной литературе используется словосочетание confidence level, CL (доверительный уровень). В русскоязычной еще иногда говорят «статистическая достоверность», но такое выражение может привести к путанице в понимании.

Отличие «популярной» фразы от истинного утверждения вот в чём. Во всяком измерении есть не только статистические, но и систематические погрешности. Описанные выше правила связи вероятностей и количества сигм работают только для статистических погрешностей — и то если к ним применимо нормальное распределение. Если статистические погрешности всегда можно обсчитать аккуратно, то систематические погрешности — это немножко искусство. Более того, из многолетнего опыта известно, что сильные систематические отклонения уж точно не описываются нормальным распределением, и потому для них эти правила пересчета не справедливы. Так что даже если экспериментаторы всё перепроверили много раз и указали систематическую погрешность, всегда остается риск, что они что-то упустили из виду. Корректно оценить этот риск невозможно, поэтому вы на самом деле не знаете, с какой истинной вероятностью ваш ответ верен.

Конечно, по умолчанию систематическим погрешностям стоит доверять, особенно если они исходят от опытных экспериментальных групп. Но вековой опыт изучения элементарных частиц показывает, что несмотря на все предосторожности регулярно случаются проколы. Бывает, что коллаборация получает результат, сильно противоречащий какой-то гипотезе, перепроверяет анализ много раз и никаких ошибок у себя не находит. Однако этот результат затем не подтверждается другими — порой намного более точными! — экспериментами. Почему первый эксперимент дал такой странный результат, что в нём было не то, где там ошибка или неучтенная погрешность — всё это зачастую так и остается непонятым (впрочем, иногда источник ошибки быстро вскрывается, как это случилось со «сверхсветовыми» нейтрино в эксперименте OPERA).

Физики к таким оборотам событий уже привыкли, поэтому каждый экспериментальный результат, сильно отличающийся от всей сложившейся к тому времени картины, вызывает оправданный скепсис. Физики так консервативны в своем отношении вовсе не потому, что они ретрограды и намертво уверовали в какую-то одну теорию, как это хотят представить опровергатели физики. Они просто научены всем предыдущим опытом в физике частиц и знают, чем это обычно кончается. Поэтому без независимого подтверждения другими экспериментами подобные сенсации они не поддерживают.

ФЭЧ в сравнении с другими науками

Надо сказать, что сформулированные выше жесткие критерии статистической достоверности характерны именно для физики элементарных частиц и некоторых смежных разделов. Во многих других разделах физики, а тем более в других дисциплинах (в особенности, в биомедицинских науках) критерии намного слабее.

Предположим, вы измерили некие данные и хотите узнать, какова вероятность того, что они «вписываются в норму». Вы проводите статистический тест, который дает вам вероятность того, что «нормальная ситуация» без какого-либо реального отклонения только за счет статистической флуктуации даст вот такое или еще более сильное отклонение. Эта вероятность называется p-значение. В биологии пороговое p-значение, ниже которого уже уверенно говорят про реальное отличие, составляет один или даже несколько процентов. В физике элементарных частиц такое отличие вообще не считают значимым, тут нет даже «указания на существование» какого-то отличия! Ответственное заявление об отличии звучит в ФЭЧ только для p-значений меньше одной двухмиллионной (то есть отклонение больше 5σ). Такой жесткий подход к достоверности утверждений выработался в ФЭЧ примерно полвека назад, в эпоху, когда экспериментаторы видели много отклонений со значимостью в районе 3σ и смело заявляли об открытии новых частиц, хотя потом эти «открытия» не подтверждались. Подробный рассказ об истоках этого критерия см. в постах Tommaso Dorigo (часть 1, часть 2).

Формула плотности заряда — GeeksforGeeks

При измерении электрических полей по различным непрерывным распределениям заряда, таким как линейное, поверхностное и объемное, мы сталкиваемся с плотностью электрического заряда. При понимании тока электричества мы также должны учитывать понятие плотности заряда. Чтобы понять плотность заряда, мы должны сначала понять эту концепцию плотности.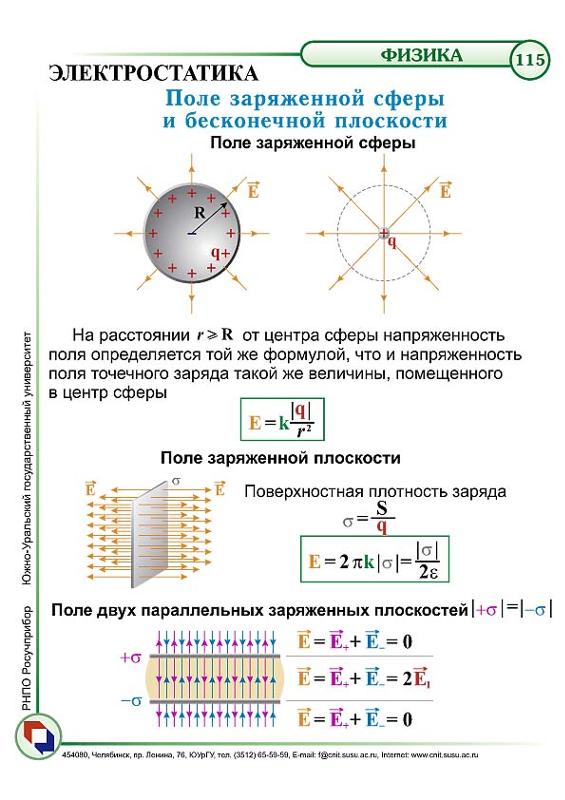 Плотность объекта определяется как его масса в единице объема. Точно так же, в зависимости от типа расположения непрерывного заряда, мы можем думать о плотности заряда как о заряде на единицу длины, поверхности или объема.

Что такое плотность заряда?

Плотность заряда определяется как количество электрического заряда, которое может быть накоплено на единице длины, площади или объема проводника. Другими словами, он указывает, сколько заряда хранится в конкретном поле. Он рассчитывает распределение заряда и может быть положительным или отрицательным.

Заряд может быть рассеян по одномерной, двумерной или трехмерной поверхности. Плотность заряда подразделяется на три типа: 

1. Линейная плотность заряда
2. Поверхностная плотность заряда и
3. Объемная плотность заряда.

Его значение прямо пропорционально количеству заряда, но изменяется обратно пропорционально размеру поверхности.

Линейная плотность заряда

Линейная плотность заряда определяется как количество заряда на единице длины проводника. Обозначается символом лямбда (λ). Его стандартной единицей измерения являются кулоны на метр (см ^-1 ), а размерная формула определяется как [M ⁰ L ^-1 T ¹ I ¹ ].

Его формула равна отношению величины заряда к длине проводящей поверхности.

λ = q/l

где,

• λ — линейная плотность заряда,
• q — заряд,
• l — длина поверхности.

Поверхностная плотность заряда

Поверхностная плотность заряда определяется как количество заряда на единице площади проводника. Обозначается символом сигма (σ). Его стандартной единицей измерения являются кулоны на квадратный метр (см ^-2 ), а размерная формула определяется как [M ⁰ L ^-2 T ¹ I ¹ ].

Его формула равна отношению величины заряда к площади проводящей поверхности.

σ = q/A

где,

• σ – поверхностная плотность заряда,
• q – заряд,
• A – площадь поверхности.

Объемная плотность заряда

Объемная плотность заряда определяется как количество заряда, присутствующего в единице объема проводника. Обозначается символом ро (ρ). Его стандартной единицей измерения являются кулоны на кубический метр (см ^-3 ), а размерная формула определяется как [M ⁰ L ^-3 T ¹ I ¹ ].

Его формула равна отношению величины заряда к объему проводящей поверхности.

ρ = q/V

где,

• σ – поверхностная плотность заряда,
• q – заряд,
• V – объем поверхности.

Примеры задач

Задача 1. Рассчитайте линейную плотность заряда поверхности, если заряд равен 2 Кл, а длина равна 4 м.

Решение:

Имеем,

q = 2 

l = 4

Используя полученную формулу,

λ = q/ л

= 2/4

= 0,5 см ^-1

Задача 2. Рассчитайте линейную плотность заряда поверхности, если заряд равен 5 Кл, а длина равна 3 м.

Решение:

Имеем,

q = 5

l = 3

Используя формулу имеем,

λ = q/l

= 5/3

= 1,67 см ^-1

Задача 3. Рассчитать заряд, если линейная плотность заряда поверхности составляет 3 см ^-1 и длина 5 м.

Решение:

Имеем,

λ = 3

l = 5

Используя полученную формулу,

λ = q/ l

=> q = λl

= 3 ( 5)

= 15 С

Задача 4. Рассчитайте поверхностную плотность заряда поверхности, если заряд равен 20 Кл, а площадь равна 10 м ² .

Решение:

Имеем,

q = 20

A = 10

Используя полученную формулу,

σ = q/A

= 20/10

= 2 см ^-2

Задача 5.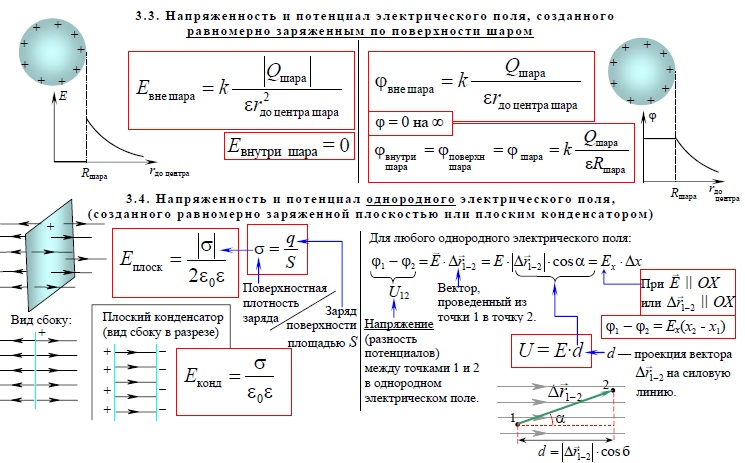 Вычислить заряд, если поверхностная плотность заряда поверхности равна 5 см ^-2 , а площадь равна 20 м ² .

Решение:

Имеем,

σ = 5 

A = 20

Используя полученную формулу,

σ = q/A

=> q = σA

= 5 ( 20)

= 100 Кл

Задача 6. Вычислить объемную плотность заряда поверхности, если заряд равен 50 Кл, а объем равен 80 м ³ .

Решение:

Имеем,

q = 50

V = 80

Используя формулу, которую мы имеем,

ρ = q/V

= 50/80

= 0,625 см ^-3 90 003

Задача 7: Рассчитать плату, если объем плотность заряда поверхности 1 см ^-3 и объема 25 м ³ .

Решение:

Имеем,

ρ = 1

V = 25

Используя полученную формулу,

ρ = q /V

=> q = ρV

= 1 (25)

= 25 C

Сигма-дырки от поверхностей изомолекулярного электростатического потенциала

. 2019 14 мая; 25 (6): 160.

doi: 10.1007/s00894-019-4051-2.

Райан Дж. Аламински
¹
, Семинар Хорхе М.
²

3

4

Принадлежности

• ¹ Факультет химического машиностроения, Техасский университет A&M, Колледж-Стейшн, Техас, 77843, США.
• ² Факультет химического машиностроения, Техасский университет A&M, Колледж-Стейшн, Техас, 77843, США. семинарио@таму.эду.
• ³ Факультет электротехники и вычислительной техники, Техасский университет A&M, Колледж-Стейшн, Техас, 77843, США. семинарио@таму.эду.
• ⁴ Факультет материаловедения и инженерии, Техасский университет A&M, Колледж-Стейшн, Техас, 77843, США. семинарио@таму.эду.

• PMID:

  31089893

• DOI:

  10.1007/s00894-019-4051-2

Ryan J Alaminsky et al.

Модель Джей Мол.

2019 .

. 2019 14 мая; 25 (6): 160.

doi: 10.1007/s00894-019-4051-2.

Авторы

Райан Дж. Аламински
¹
, Семинар Хорхе М.
²

3

4

Принадлежности

• ¹ Факультет химического машиностроения, Техасский университет A&M, Колледж-Стейшн, Техас, 77843, США.
• ² Факультет химического машиностроения, Техасский университет A&M, Колледж-Стейшн, Техас, 77843, США. семинарио@таму.эду.
• ³ Факультет электротехники и вычислительной техники, Техасский университет A&M, Колледж-Стейшн, Техас, 77843, США. семинарио@таму.эду.
• ⁴ Факультет материаловедения и инженерии, Техасский университет A&M, Колледж-Стейшн, Техас, 77843, США. семинарио@таму.эду.

• PMID:

  31089893

• DOI:

  10. 1007/s00894-019-4051-2

Абстрактный

Визуализация области σ-дырок молекул галогенбензола (PhX, X = Cl, Br, I) была проведена для исследования природы σ-дырки, присутствующей между ковалентно связанными элементами групп IVB-VIIB (известной как галогенная связь для группы VIIB). ) и соответствующие отрицательные сайты, такие как неподеленные электронные пары с основанием Льюиса, π-электроны или анионы. σ-дырка состоит из области с низкой электронной плотностью и часто относительно положительным электростатическим потенциалом, окружающей самую внешнюю часть атома галогена вдоль оси связи AX. В этой работе исследуются изоповерхности молекулярного электростатического потенциала (МЭП) для PhX, полученные из расчетов ab initio, для определения σ-дырки в 3D, показывая поверхности соответствующих положительных и отрицательных областей. Поверхности были картированы для изопотенциалов молекул PhX от 0,003 В и увеличены в 10 раз до 3 В. σ-дырка проявляется как положительная область, обнаженная под преимущественно отрицательной изоповерхностью МЭП. По мере удаления значений изопотенциала от нуля радиус этой дыры увеличивается; и наоборот, его присутствие полностью исчезает, когда потенциал приближается к нулю с увеличением расстояния от молекулы. Этот метод также можно использовать для сравнения поведения нейтральных молекул и их ионных аналогов, например, в случае нейтрального PF 9.0427 6 (экспериментально не наблюдалось) и анион гексафторфосфата, PF ₆ ^— , типичный противоион в коммерческих литий-ионных батареях. Галогенид пниктогена PF ₅ имеет те же тенденции MEP, что и нейтральный PF ₆ , который имеет реакционные центры, показанные в виде отрицательных потенциалов, в определенных точках молекулы, аналогичные таковым у PF ₅ . Изображение поведения МЭП на изоповерхностях при конкретных и практических значениях, представляющих химический интерес, имеет решающее значение при определении наборов групповых параметров для кулоновских силовых полей для моделирования молекулярной динамики, которые будут использоваться в системах, которые переходят от биологических макромолекул к инженерии кристаллов, устройствам и конечным продуктам. . Активные химические центры могут быть описаны с помощью функции MEP V (r) более точно, чем просто волновые функции или плотности электронов, которые по своей сути содержат ту же информацию, и это полностью усиливается, когда показаны плотности электронов с цветовым кодированием на изопотенциальных поверхностях. Графический реферат Скрытые особенности орбитальных дыр, изображаемые изопотенциалами.

Ключевые слова:

ДПФ; Изо-плотность; изопотенциал; МООС; Отверстие сигмы.

Похожие статьи

• Связь σ-дырок: физическая интерпретация.

  Политцер П., Мюррей Дж.С., Кларк Т.

  Полицер П. и др.
  Top Curr Chem. 2015;358:19-42. дои: 10.1007/128_2014_568.
  Top Curr Chem. 2015.

  PMID: 25467532

• Светлое будущее нетрадиционных взаимодействий σ/π-дырок.

  Bauzá A, Mooibroek TJ, Frontera A.

  Бауза А. и др.
  Химфиз. 2015 24 августа; 16 (12): 2496-517. doi: 10.1002/cphc.201500314. Epub 2015 26 июня.
  Химфиз. 2015.

  PMID: 26118675

• Галогенная связь: сигма-дырка. Материалы «Моделирование взаимодействий в биомолекулах II», Прага, 5-9 сентября.т, 2005.

  Кларк Т., Хеннеманн М., Мюррей Дж.С., Политцер П.

  Кларк Т. и др.
  Модель Джей Мол. 2007 Февраль; 13 (2): 291-6. doi: 10.1007/s00894-006-0130-2. Epub 2006 23 августа.
  Модель Джей Мол. 2007.

  PMID: 16927107

• Связь пниктогена: ковалентно связанный атом мышьяка в молекулярных образованиях в кристаллах как донор связи пниктогена.

  Варадвадж А., Варадвадж П. Р., Маркес Х.М., Ямашита К.

  Варадвадж А. и соавт.
  Молекулы. 2022 25 мая; 27 (11): 3421. дои: 10.3390/молекулы27113421.
  Молекулы. 2022.

  PMID: 35684359
  Бесплатная статья ЧВК.

  Обзор.

• Нековалентные связи через сигму и пи-дырку, расположенные на одной и той же молекуле. Руководящие принципы и сравнения.

  Зиркевич В., Михальчик М., Шайнер С.

  Зиркевич В. и соавт.
  Молекулы. 2021 20 марта; 26 (6): 1740. doi: 10,3390/молекулы 26061740.
  Молекулы. 2021.

  PMID: 33804617
  Бесплатная статья ЧВК.

  Обзор.

Посмотреть все похожие статьи

Рекомендации

1. 1. Chem Rev. 12 января 2000 г .; 100 (1): 143–68.

      —

      пабмед

2. 1. J Comput Chem.